题目内容
19.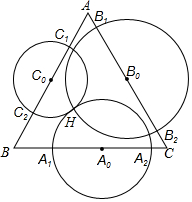 已知H是锐角△ABC的垂心,以边BC的中点为圆心、过点H的圆与直线BC交于A1,A2两点,以边CA的中点为圆心、过点H的圆与直线CA交于B1、B2两点,以边AB的中点为圆心、过点H的圆与直线AB交于C1、C2两点,证明:A1,A2,B1,B2,C1,C2六点共圆.
已知H是锐角△ABC的垂心,以边BC的中点为圆心、过点H的圆与直线BC交于A1,A2两点,以边CA的中点为圆心、过点H的圆与直线CA交于B1、B2两点,以边AB的中点为圆心、过点H的圆与直线AB交于C1、C2两点,证明:A1,A2,B1,B2,C1,C2六点共圆.
分析 作出辅助线,先判断出A'H⊥BC,再用切割线定理得出AC1×AC2=AA'×AH=AB1×AB2,从而判断出B1,B2,C1,C2四点共圆.最后判断出OB1=OB2=OC1=OC2.同理可得,OA1=OA2=OB1=OB2,结论得证.
解答 证明:如图,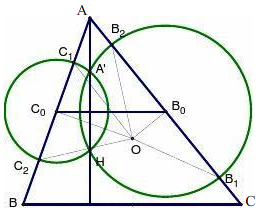
∵B0,C0分别是边CA,AB的中点.
设以边B0为圆心,过点H的圆与以C0为圆心,过点H的圆的另一个交点为A',
则A'H⊥C0B0.
∵B0,C0分别是边CA,AB的中点,
∴C0B0∥BC,从而A'H⊥BC,
于是点A'在AH上.
由切割线定理:
AC1×AC2=AA'×AH=AB1×AB2,
∴B1,B2,C1,C2四点共圆.
分别作B1B2,C1C2的垂直平分线,设它们相交于点O,则O是四边形B1B2C1C2的外心,
且OB1=OB2=OC1=OC2.
同理可得,OA1=OA2=OB1=OB2,
A1,A2,B1,B2,C1,C2六点都是在以O为圆心,OA1为半径的圆上,
故六点A1,A2,B1,B2,C1,C2共圆.
点评 此题是三角形的五心,主要考查了切割线定理,四点共圆,线段的垂直平分线三角形的外心,判断四点共圆是解本题的关键,难点是作出辅助线.是一道特别难的竞赛题.

练习册系列答案
相关题目
7.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
下列说法:
①抛物线的开口向下;
②当x>-3时,y随x的增大而增大;
③二次函数的最小值是-2;
④抛物线的对称轴是x=-2.5,
其中正确的是④(填序号)
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
①抛物线的开口向下;
②当x>-3时,y随x的增大而增大;
③二次函数的最小值是-2;
④抛物线的对称轴是x=-2.5,
其中正确的是④(填序号)
14.下列各式中,属于二元一次方程的是( )
| A. | x2+y=0 | B. | x=$\frac{2}{y}$+1 | C. | $\frac{x+y}{3}$-2y=1 | D. | y+2x |
 二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+a的图象不经过第四象限.
二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+a的图象不经过第四象限.
 如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( ) 如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3$\sqrt{2}$,BG=4,则GH的长为$\frac{8\sqrt{10}}{11}$.
如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3$\sqrt{2}$,BG=4,则GH的长为$\frac{8\sqrt{10}}{11}$.