题目内容
13．二次函数y=x2-2x+b的对称轴是直线x=1．分析 将二次函数配方成顶点式即可确定对称轴方程．
解答 解：∵y=x2-2x+b
=x2-2x+1+b-1
=（x+1）2+b-1
故对称轴是直线x=1．
故答案为：1．
点评 本题考查了二次函数的性质，解题的关键是能够对二次函数进行配方，也可以利用对称轴公式，难度不大．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
4．cos30°的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
1．抛物线y=-x2+6x-9的顶点为A，与y轴的交点为B，如果在抛物线上取点C，在x轴上取点D，使得四边形ABCD为平行四边形，那么点D的坐标是（ ）
| A． | （-6，0） | B． | （6，0） | C． | （-9，0） | D． | （9，0） |
5．若圆锥的底面半径为3cm，展开后所得扇形的半径为4cm，则它的侧面积等于（ ）
| A． | 12πcm2 | B． | 6πcm2 | C． | 12cm2 | D． | 24πcm |
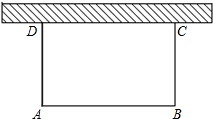如图，用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD，已知墙长14m，设边AD的长为x（m），矩形ABCD的面积为y（m2）．