题目内容
2.已知直线l:y=x,抛物线C:y=x2+bx+c.(1)当b=4,c=1时,求直线l与抛物线C的交点坐标;
(2)当b=$\sqrt{3}$,c=-4时,将直线l绕原点逆时针旋转15°后与抛物线C交于A,B两点(A点在B点的左侧),求A,B两点的坐标;
(3)若将(2)中的条件“c=-4”去掉,其他条件不变,且2≤AB≤4,求c的取值范围.
分析 (1)联立方程,解方程求得即可;
(2)由题意得旋转后的直线的解析式为y=$\sqrt{3}$x,然后联立方程,解方程求得即可;
(3)根据题意求得$\frac{4ac-{b}^{2}}{4a}$交点坐标,然后根据勾股定理表示出AB,得出不等式,解不等式即可求得c的取值范围.
解答 解:(1)∵b=4,c=1,
∴抛物线C:y=x2+4x+1.
解$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}+4x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{-3+\sqrt{5}}{2}}\\{y=\frac{-3+\sqrt{5}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{-3-\sqrt{5}}{2}}\\{y=\frac{-3-\sqrt{5}}{2}}\end{array}\right.$,
∴直线l与抛物线C的交点坐标是($\frac{-3+\sqrt{5}}{2}$,$\frac{-3+\sqrt{5}}{2}$)或($\frac{-3-\sqrt{5}}{2}$,$\frac{-3-\sqrt{5}}{2}$);
(2)设直线绕原点逆时针旋转15°得到直线AB,
而直线l与x轴的夹角为45°,
∴旋转后直线AB与x轴的夹角为60°,
∴旋转后的直线AB的解析式为y=$\sqrt{3}$x,
解$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{y={x}^{2}+\sqrt{3}x-4}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=2\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-2\sqrt{3}}\end{array}\right.$,
∴A(-2,-2$\sqrt{3}$),B(2,2$\sqrt{3}$);
(3)$\left\{\begin{array}{l}{y={x}^{2}+\sqrt{3}x+c}\\{y=\sqrt{3}x}\end{array}\right.$
整理得,x2+c=0,
解得x=±$\sqrt{-c}$,
∴A(-$\sqrt{-c}$,-$\sqrt{-3c}$),B($\sqrt{-c}$,$\sqrt{-3c}$),
∴AB=$\sqrt{({\sqrt{-c}+\sqrt{-c})}^{2}+({\sqrt{-3c}+\sqrt{-3c})}^{2}}$=4$\sqrt{-c}$,
∵2≤AB≤4,
∴2≤4$\sqrt{-c}$≤4,
∴-1≤c≤-$\frac{1}{4}$.
点评 本题考查二次函数的图象与几何变换,反比例函数与一次函数的交点,反比例函数与一次函数图象的交点坐标满足两函数解析式.

| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
| A. | y=$\frac{6}{x}$ | B. | y=$\frac{x}{6}$ | C. | y=x2 | D. | y=$\frac{x+1}{6}$ |
 根据有理数a,b在数轴上的位置(如图),则有下列六个不等式:①a-b>0;②a+b<0;③ab<0;④b2-a2>0;⑤$\frac{1}{a}$-$\frac{1}{b}$<0;⑥|a|-|b|>0,其中错误的是②③④⑥(只填序号).
根据有理数a,b在数轴上的位置(如图),则有下列六个不等式:①a-b>0;②a+b<0;③ab<0;④b2-a2>0;⑤$\frac{1}{a}$-$\frac{1}{b}$<0;⑥|a|-|b|>0,其中错误的是②③④⑥(只填序号).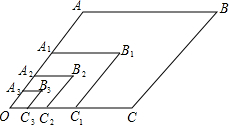 如图,在菱形OABC中,∠AOC=60°,OA=2$\sqrt{2}$,以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OABC缩小,得到菱形OA1B1C1;再以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OA1B1C1缩小,得到菱形OA2B2C2;…,以此类推,则菱形OA2016B2016C2016的面积为$\sqrt{6}$×($\frac{1}{2}$)4032.
如图,在菱形OABC中,∠AOC=60°,OA=2$\sqrt{2}$,以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OABC缩小,得到菱形OA1B1C1;再以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OA1B1C1缩小,得到菱形OA2B2C2;…,以此类推,则菱形OA2016B2016C2016的面积为$\sqrt{6}$×($\frac{1}{2}$)4032.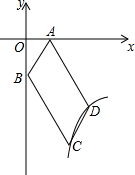 如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).
如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).