题目内容
4.如图,在边长为$\sqrt{3}$+1的菱形ABCD中,∠A=60°,点E,F分别在AB,AD上,沿EF折叠菱形,使点A落在BC边上的点G处,且EG⊥BD于点M,则EG的长为$\sqrt{3}$.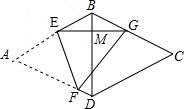
分析 首先连接AC,在Rt△ABO中,求出AO的长度,进而求出AC的长度是多少;然后根据EG⊥BD,AC⊥BD,可得EG∥AC,所以$\frac{EG}{AC}=\frac{BE}{AB}$,据此求出EG的长为多少即可.
解答 解:如图1,连接AC,交BD于点O,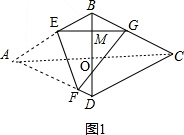 ,
,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,
∵∠A=60°,
∴∠BAO=30°,
∴AO=AB•cos30°=($\sqrt{3}$+1)×$\frac{\sqrt{3}}{2}$=$\frac{3+\sqrt{3}}{2}$,
∴AC=$\frac{3+\sqrt{3}}{2}$×2=3$+\sqrt{3}$,
∵沿EF折叠菱形,使点A落在BC边上的点G处,
∴EG=AE,
∵EG⊥BD,AC⊥BD,
∴EG∥AC,
∴$\frac{EG}{AC}=\frac{BE}{AB}$,
又∵EG=AE,
∴$\frac{EG}{3+\sqrt{3}}=\frac{\sqrt{3}+1-EG}{\sqrt{3}+1}$,
解得EG=$\sqrt{3}$,
∴EG的长为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 (1)此题主要考查了翻折变换问题,要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了菱形的性质和应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.

练习册系列答案
相关题目
14.如果两圆的半径分别为6和4,圆心距为7,那么这两圆的位置关系是( )
| A. | 内含 | B. | 内切 | C. | 相交 | D. | 外切 |
12.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{\sqrt{2}}{4}$ | D. | 2$\sqrt{2}$ |
9.下列事件为必然事件的是( )
| A. | 经过有交通信号灯的路口,遇到红灯 | |
| B. | 明天一定会下雨 | |
| C. | 抛出的篮球会下落 | |
| D. | 任意买一张电影票,座位号是2的倍数 |
13. 正比例函数y=kx的图象如图所示,则k的取值范围是( )
正比例函数y=kx的图象如图所示,则k的取值范围是( )
 正比例函数y=kx的图象如图所示,则k的取值范围是( )
正比例函数y=kx的图象如图所示,则k的取值范围是( )| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
14.据统计,2015年在“情系桃源,好运丹东”的鸭绿江桃花观赏活动中,6天内参与人次达27.8万.用科学记数法将27.8万表示为( )
| A. | 2.78×106 | B. | 27.8×106 | C. | 2.78×105 | D. | 27.8×105 |
 如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=6cm时,BC与⊙A相切.
如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=6cm时,BC与⊙A相切.