题目内容
20.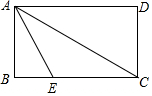 如图,在矩形纸片ABCD中,点E在BC上,且AE=EC=2.若将纸片沿AE折叠,点B好落在AC上,则AC等于( )
如图,在矩形纸片ABCD中,点E在BC上,且AE=EC=2.若将纸片沿AE折叠,点B好落在AC上,则AC等于( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
分析 根据等腰三角形的性质得到∠EAC=∠ECA,根据翻折变换的性质得到∠BAE=∠EAC,根据三角形内角和定理得到∠BAE=∠EAC=∠ECA=30°,根据直角三角形的性质和勾股定理计算即可.
解答 解:∵AE=EC,
∴∠EAC=∠ECA,
∵将纸片沿AE折叠,点B好落在AC上,
∴∠BAE=∠EAC,
∴∠BAE=∠EAC=∠ECA=30°,
∴BE=$\frac{1}{2}$AE=1,BC=BE+EC=3,
由勾股定理得,AB=$\sqrt{3}$,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{3}$,
故选:C.
点评 本题考查的是翻折变换的性质、矩形的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
15.下列四组线段中,不是成比例线段的是( )
| A. | a=3,b=6,c=2,d=4 | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{6}$,d=2$\sqrt{3}$ | ||
| C. | a=4,b=6,c=5,d=10 | D. | a=2,b=$\sqrt{5}$,c=$\sqrt{15}$,d=2$\sqrt{3}$ |
12.如图,移动小菱形◇可以得到美丽的“中国结”图案,如图三个图案是由小菱形◇平移后得到的类似“中国结”的图案,如果按图中的规律,那么第10个图案中,小菱形◇有( )
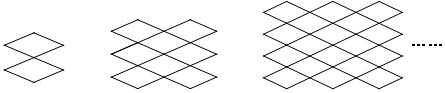

| A. | 62个 | B. | 162个 | C. | 184个 | D. | 200个 |
 ;
;