题目内容
10.若$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$与$\left\{\begin{array}{l}{x=3}\\{y=c}\end{array}\right.$都是方程x+y=b(b≠0)的解,则c=-1.分析 根据方程解的定义,把x=1,y=1代入x+y=b(b≠0),求得b,再把x=3,y=c代入即可得出c的值.
解答 解:∵$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$与$\left\{\begin{array}{l}{x=3}\\{y=c}\end{array}\right.$都是方程x+y=b(b≠0)的解,
∴2=b,把b=2代入得x+y=2,
再把x=3,y=c代入x+y=2,得c=-1,
故答案为-1.
点评 本题考查了二元一次方程的解,掌握二元一次方程组的解是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.给出下列函数:(1)y=2x;(2)y=-2x+1;(3)y=$\frac{2}{x}$.其中,y随x的增大而减小的函数是( )
| A. | (1)、(2) | B. | (1)、(3) | C. | (2)、(3) | D. | (1)、(2)、(3) |
1. 如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
 如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )| A. | AB⊥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
18.下列四组等式变形中,正确的是( )
| A. | 由5x+7=0,得5x=-7 | B. | 由2x-3=0,得2x-3+3=0 | ||
| C. | 由$\frac{x}{6}$=2,得x=$\frac{1}{3}$ | D. | 由5x=7.得x=$\frac{5}{7}$ |
5.下列各式是二元一次方程的是( )
| A. | x=3y | B. | 2x+y=3z | C. | x2+x-y=0 | D. | 3X+2=5 |
20.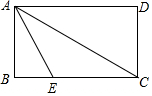 如图,在矩形纸片ABCD中,点E在BC上,且AE=EC=2.若将纸片沿AE折叠,点B好落在AC上,则AC等于( )
如图,在矩形纸片ABCD中,点E在BC上,且AE=EC=2.若将纸片沿AE折叠,点B好落在AC上,则AC等于( )
 如图,在矩形纸片ABCD中,点E在BC上,且AE=EC=2.若将纸片沿AE折叠,点B好落在AC上,则AC等于( )
如图,在矩形纸片ABCD中,点E在BC上,且AE=EC=2.若将纸片沿AE折叠,点B好落在AC上,则AC等于( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
 如图,已知OA=OB.则数轴上点A所表示的数a是-$\sqrt{10}$;
如图,已知OA=OB.则数轴上点A所表示的数a是-$\sqrt{10}$;