题目内容
 如图,已知∠DAB=∠CBE=90°,点E是线段AB的中点,CE平分∠DCB且与DA的延长线相交于点F,求证:DE平分∠FDC.
如图,已知∠DAB=∠CBE=90°,点E是线段AB的中点,CE平分∠DCB且与DA的延长线相交于点F,求证:DE平分∠FDC.考点:角平分线的性质
专题:证明题
分析:过点E作EH⊥CD,根据角平分线上的点到角的两边距离相等可得BE=EH,再根据线段中点的定义可得AE=BE,然后求出AE=EH,再根据到角的两边距离相等的点在角的平分线上证明即可.
解答: 证明:过点E作EH⊥CD,
证明:过点E作EH⊥CD,
∵CE平分∠DCB,∠CBE=90°,
∴BE=EH,
∵点E是线段AB的中点,
∴AE=BE,
∴AE=EH,
又∵∠DAB=90°,
∴DE平分∠FDC.
 证明:过点E作EH⊥CD,
证明:过点E作EH⊥CD,∵CE平分∠DCB,∠CBE=90°,
∴BE=EH,
∵点E是线段AB的中点,
∴AE=BE,
∴AE=EH,
又∵∠DAB=90°,
∴DE平分∠FDC.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记性质并作出辅助线是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
下列说法中,正确的是( )
| A、若a表示有理数,则-a表示负有理数 |
| B、多项式3πa3+4a2-8的次数是4 |
| C、有理数分为正有理数和负有理数 |
| D、两个数绝对值相等,则这两个数相等或互为相反数. |
绝值大于1而小于5的整数有( )
| A、7个 | B、6个 | C、5个 | D、4个 |
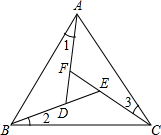 如图,已知在△ABC中,∠BAC=∠ACB=∠CBA,∠1=∠2=∠3.
如图,已知在△ABC中,∠BAC=∠ACB=∠CBA,∠1=∠2=∠3.