题目内容
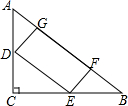如图，在△ABC中作一个长方形DEFG，D、E分别在AC、BE上，F、G在AB上，若∠C=90°，AC=3cm，BC=4cm，求长方形DEFG的最大面积．考点：相似三角形的判定与性质,二次函数的最值
专题：常规题型
分析：设CE=x，则EB=4-x，根据三角形相似即可用x表示EF和EG的长度，求关于x函数式的最大值即可解题．
解答：解：设CE=x，则EB=4-x，
∵长方形DEFG，
∴△ABC∽△DCE，△EFB∽△ACB，
∴
=
，DE=
x，
=
，EF=
，
∴长方形DEFG的面积=EF•DE=
=
，
当x=2时，长方形DEFG的面积有最大值3．
∵长方形DEFG，
∴△ABC∽△DCE，△EFB∽△ACB，
∴
| DE |
| AB |
| CE |
| BC |
| 5 |
| 4 |
| EF |
| AC |
| BE |
| AB |
| 12-3x |
| 5 |
∴长方形DEFG的面积=EF•DE=
| -3x2+12 |
| 4 |
| -3(x-2)2+12 |
| 4 |
当x=2时，长方形DEFG的面积有最大值3．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比值相等的性质．
练习册系列答案
阅读快车系列答案
相关题目
下面四个式子：-120=-20；（-3）4÷（-3）3=3；（-
）2-
=0；9÷9×
=9中，其中不正确的有（ ）
| 2 |
| 3 |
| 22 |
| 32 |
| 1 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
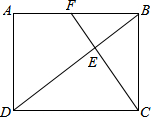如图，在矩形ABCD中，CF⊥BD于点E，交AB于点F，如果F是AB的中点，则AD：AB=
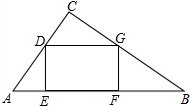如图，在△ABC中，∠C=90°，AC=6，BC=8，四边形DEFG是它的内接矩形，点D在边AC上，点E、F在边AB上，点G在边BC上，当CD=
尺规作图：（不写作法，保留作图痕迹）已知线段a、b和∠α．
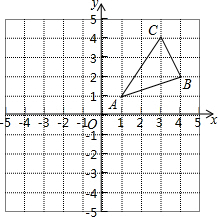如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．