题目内容
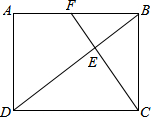如图，在矩形ABCD中，CF⊥BD于点E，交AB于点F，如果F是AB的中点，则AD：AB=考点：相似三角形的判定与性质,矩形的性质
专题：常规题型
分析：在矩形ABCD中，CF⊥BD，易证得△BCD∽△FBC，根据相似三角形的对应边成比例，可得AD：AB的值．
解答：解：∵四边形ABCD为矩形，
∴∠BCF+∠DCF=90°，
∵CF⊥BD，
∴∠BDC+∠DCF=90°，
∴∠BDC=∠BCF，
∴△BCD∽△FBC，
∴
=
，
∵AB=2BF，
∴AD：AB=
：2．
∴∠BCF+∠DCF=90°，
∵CF⊥BD，
∴∠BDC+∠DCF=90°，
∴∠BDC=∠BCF，
∴△BCD∽△FBC，
∴
| BC |
| CD |
| BF |
| BC |
∵AB=2BF，
∴AD：AB=
| 2 |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
全程金卷系列答案
相关题目
如图，四边形ABCD中，∠BAD=110°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小，此时∠MAN的度数为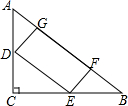
如图，在△ABC中作一个长方形DEFG，D、E分别在AC、BE上，F、G在AB上，若∠C=90°，AC=3cm，BC=4cm，求长方形DEFG的最大面积．
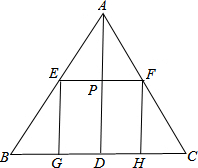△ABC中，已知BC=6，点D是BC边上的中点，AD=5，点P为线段AD上一点（与A、D不重合），过P作EF∥BC分别交AB，AC于点E、F，过E、F分别作EG∥AD，FH∥AD交BC边于点G．
如图所示，已知AB为⊙O的直径，半径OC⊥AB，E为OB上一点，弦AD⊥CE交OC于点F，猜想OE与OF的数量关系，并说明你的理由．