题目内容
解下列方程:
(1)x2-2x-1=0;
(2)2x2-5x-1=0;
(3)x2-3x-18=0;
(4)4x(x+1)=x2-1.
(1)x2-2x-1=0;
(2)2x2-5x-1=0;
(3)x2-3x-18=0;
(4)4x(x+1)=x2-1.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)利用求根公式法求解即可;
(2)利用求根公式法求解;
(3)利用十字相乘法分解因式,然后求解即可;
(4)先移项并分解因式,然后求解即可.
(2)利用求根公式法求解;
(3)利用十字相乘法分解因式,然后求解即可;
(4)先移项并分解因式,然后求解即可.
解答:解:(1)配方得,(x2-2x+1)-1-1=0,
即(x-1)2=2,
所以,x-1=±
,
x1=1+
,x2=1-
;
(2)a=2,b=-5,c=-1,
△=b2-4ac=(-5)2-4×2×(-1)=25+8=33,
x=
=
,
x1=
,x2=
;
(3)因式分解得,(x+3)(x-6)=0,
由此得,x+3=0,x-6=0,
所以,x1=-3,x2=6;
(4)移项得,4x(x+1)-(x2-1)=0,
因式分解得,4x(x+1)-(x+1)(x-1)=0,
(x+1)(3x+1)=0,
由此得x+1=0,3x+1=0,
所以x1=-1,x2=-
.
即(x-1)2=2,
所以,x-1=±
| 2 |
x1=1+
| 2 |
| 2 |
(2)a=2,b=-5,c=-1,
△=b2-4ac=(-5)2-4×2×(-1)=25+8=33,
x=
-(-5)±
| ||
| 2×2 |
5±
| ||
| 4 |
x1=
5+
| ||
| 4 |
5-
| ||
| 4 |
(3)因式分解得,(x+3)(x-6)=0,
由此得,x+3=0,x-6=0,
所以,x1=-3,x2=6;
(4)移项得,4x(x+1)-(x2-1)=0,
因式分解得,4x(x+1)-(x+1)(x-1)=0,
(x+1)(3x+1)=0,
由此得x+1=0,3x+1=0,
所以x1=-1,x2=-
| 1 |
| 3 |
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
 如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为
如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为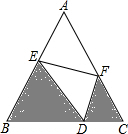 如图,已知D为BC上一点,∠B=∠C=∠EDF=60°,BE=6,CD=3,CF=4,求AF的长.
如图,已知D为BC上一点,∠B=∠C=∠EDF=60°,BE=6,CD=3,CF=4,求AF的长.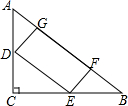 如图,在△ABC中作一个长方形DEFG,D、E分别在AC、BE上,F、G在AB上,若∠C=90°,AC=3cm,BC=4cm,求长方形DEFG的最大面积.
如图,在△ABC中作一个长方形DEFG,D、E分别在AC、BE上,F、G在AB上,若∠C=90°,AC=3cm,BC=4cm,求长方形DEFG的最大面积. 如图,正方形纸片ABCD的面积为1,点M、N分别在AD、BC上,且AM=BN=
如图,正方形纸片ABCD的面积为1,点M、N分别在AD、BC上,且AM=BN=