题目内容
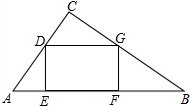如图，在△ABC中，∠C=90°，AC=6，BC=8，四边形DEFG是它的内接矩形，点D在边AC上，点E、F在边AB上，点G在边BC上，当CD=| 1 |
| 2 |
考点：相似三角形的判定与性质
专题：
分析：易证△BGF∽△BAC，即可求得FG的值，在根据△ADE∽△ABC即可解题．
解答：解：∵∠B=∠B，∠BFG=∠BCA，
∴△BGF∽△BAC，
∴
=
，
∵S△BGF=
S△ABC
∴GF•
GF=24，GF=3
，
∵∠A=∠A，∠AED=∠BCA，
∴△ADE∽△ABC，
∴
=
=
，
∴AD=
，CD=AC-AD=6-
．
∴△BGF∽△BAC，
∴
| GF |
| BF |
| 3 |
| 4 |
∵S△BGF=
| 1 |
| 2 |
∴GF•
| 4 |
| 3 |
| 2 |
∵∠A=∠A，∠AED=∠BCA，
∴△ADE∽△ABC，
∴
| DE |
| AD |
| BC |
| AB |
| 4 |
| 5 |
∴AD=
15
| ||
| 4 |
15
| ||
| 4 |
点评：本题考查了相似三角形的判定和相似三角形对应边比例相等的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
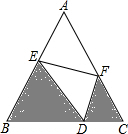如图，已知D为BC上一点，∠B=∠C=∠EDF=60°，BE=6，CD=3，CF=4，求AF的长．
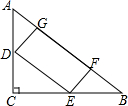如图，在△ABC中作一个长方形DEFG，D、E分别在AC、BE上，F、G在AB上，若∠C=90°，AC=3cm，BC=4cm，求长方形DEFG的最大面积．
利用网格线作图：
如图，正方形纸片ABCD的面积为1，点M、N分别在AD、BC上，且AM=BN=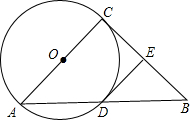
如图，以Rt△ABC的直角边AC为直径作⊙O，交AB于D，E为BC中点，求证：DE是⊙O的切线．