题目内容
15.计算:(1)(4$\sqrt{6}$-2$\sqrt{2}$+6$\sqrt{2}$)÷2$\sqrt{2}$
(2)$\frac{2}{b}$$\sqrt{a{b}^{5}}$•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)•$\frac{1}{3}$$\sqrt{\frac{a}{b}}$.
分析 (1)直接利用二次根式除运算法则得出答案;
(2)直接利用二次根式乘法运算法则得出答案.
解答 解:(1)(4$\sqrt{6}$-2$\sqrt{2}$+6$\sqrt{2}$)÷2$\sqrt{2}$
=(4$\sqrt{6}$+4$\sqrt{2}$)÷2$\sqrt{2}$
=2$\sqrt{3}$+2;
(2)$\frac{2}{b}$$\sqrt{a{b}^{5}}$•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)•$\frac{1}{3}$$\sqrt{\frac{a}{b}}$
=-$\frac{2}{b}$×$\frac{3}{2}$×$\frac{1}{3}$$\sqrt{a{b}^{5}×{a}^{3}b×\frac{a}{b}}$
=-$\frac{1}{b}$•a2b2$\sqrt{ab}$
=-a2b$\sqrt{ab}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
3.化简:
| (1)$\sqrt{72}$; | (2)$\sqrt{48}$; | (3)$\sqrt{\frac{2}{3}}$; |
| (4)-2$\sqrt{\frac{9}{2}}$; | (5)$\sqrt{{a}^{3}b}$(a≤0); | (6)$\sqrt{{a}^{4}+2{a}^{2}{b}^{2}+{b}^{4}}$. |
3.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解是( )
| A. | x1=0 x2=4 | B. | x1=1 x2=5 | C. | x1=1 x2=-5 | D. | x1=-1 x2=5 |
20.两个三角形有以下元素对应相等,则不能确定全等的是( )
| A. | SSA | B. | SAS | C. | AAS | D. | SSS |

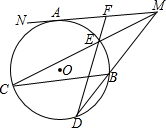 己知:⊙O与直线MN相切于A点,弦BC∥MN,直线MB与⊙O相交于D点,MC与⊙O相交于E,DE的延长线交MN于F点.求证:AF=FM.
己知:⊙O与直线MN相切于A点,弦BC∥MN,直线MB与⊙O相交于D点,MC与⊙O相交于E,DE的延长线交MN于F点.求证:AF=FM. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论: