题目内容
8.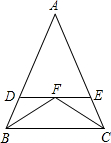 如图,△ABC中AB=AC,BF、CF分别平分∠ABC、∠ACB,过点F作直线DE∥BC,交AB、AC于D、E,则图中共有等腰三角形( )个.
如图,△ABC中AB=AC,BF、CF分别平分∠ABC、∠ACB,过点F作直线DE∥BC,交AB、AC于D、E,则图中共有等腰三角形( )个.| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
分析 先由已知运用角平分线及平行线的性质找出相等的角,再根据等角对等边找出等腰三角形.
解答 解:∵AB=AC,∠ABC、∠ACB的平分线相交于点F,
∴∠ABF=∠FBC=∠BCF=∠FCE,
∴△DBF、△FBC、△FEC是等腰三角形,
∵AB=AC,
∴∠ABC=∠ACB,且△ABC是等腰三角形,
∵EF∥BC,
∴∠AED=∠ADE=∠ABC,
∴△AED是等腰三角形.
所以共有△EBF、△FBC、△FEC、△ABC、△AED,共5个等腰三角形.
故选B.
点评 本题考查了等腰三角形的判定,有两个角相等的三角形是等腰三角形;找出相等的角是解答本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.如果|a|+a+|b|=10,|a|+|b|-b=14,那么a+b的值为( )
| A. | 0 | B. | 4 | C. | -4 | D. | -1 |
16.下面各角能成为某多边形的内角和的是( )
| A. | 430° | B. | 4320° | C. | 4334° | D. | 4360° |
3.如果将抛物线y=x2+2向左平移1个单位,那么所得新抛物线的解析式为( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=x2+1 | D. | y=x2+3 |
17.下列各式中,不是同类项的是( )
| A. | $\frac{1}{2}$ab和5ba | B. | a3和53 | C. | $\frac{xy}{5}$和52xy | D. | 102和$\frac{1}{10}$ |