题目内容
6.一个三角形的三边长分别是xcm、(x+1)cm、(x+2)cm,它的周长不超过10cm,则x的取值范围是( )| A. | x$≤\frac{13}{3}$ | B. | 1$<x≤\frac{13}{3}$ | C. | x$≤\frac{7}{3}$ | D. | 1$<x≤\frac{7}{3}$ |
分析 根据三角形的三边关系得出x+2<x+x+1,根据三角形的周长得出x+x+1+x+2≤10,求出两不等式解集的公共部分即可.
解答 解:∵三角形的三边长分别是xcm、(x+1)cm、(x+2)cm,它的周长不超过10cm,
∴x+2<x+x+1,x+x+1+x+2≤10,
解得:x>1,x≤$\frac{7}{3}$,
所以x的取值范围是1<x≤$\frac{7}{3}$,
故选D.
点评 本题考查了解一元一次不等式组,三角形三边关系定理,解一元一次不等式的应用,解此题的关键是能根据题意得出两个不等式,难度适中.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
17.下列选项的值介于0.2与0.3之间的是( )
| A. | $\sqrt{4.84}$ | B. | $\sqrt{0.484}$ | C. | $\sqrt{0.0484}$ | D. | $\sqrt{0.00484}$ |
14.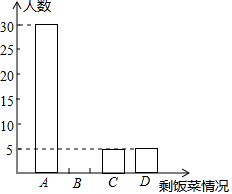 自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
(1)这次被抽查的学生有多少人?
(2)求表中m,n的值,并补全条形统计图;
(3)该中学有学生2200名,请估计这餐晚饭有剩饭的学生人数,按平均每人剩10克米饭计算,这餐晚饭将浪费多少千克米饭?
 自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:| 选项 | 频数 | 频率 |
| A | 30 | M |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | 5 | 0.1 |
(2)求表中m,n的值,并补全条形统计图;
(3)该中学有学生2200名,请估计这餐晚饭有剩饭的学生人数,按平均每人剩10克米饭计算,这餐晚饭将浪费多少千克米饭?
16.为了直观地表示世界七大洲的面积各占全球陆地面积的百分比,最适合使用的统计图是( )
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
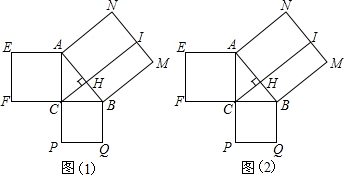
 如图,AD是△ABC的一条中线,若BD=3,则BC=6.
如图,AD是△ABC的一条中线,若BD=3,则BC=6.