题目内容
20．
如图，在平行四边形ABCD中，AB=5cm，Bc=8cm，∠BAD=120°，CE⊥AB于E，求平行四边形ABCD的面积．
分析 根据平行四边形的性质得到∠B=60°，由已知条件得到∠CEB=90°，求得CE=BC•sin60°=4$\sqrt{3}$，然后根据平行四边形的面积公式即可得到结果．
解答 解：在平行四边形ABCD中，
∵∠BAD=120°，
∴∠B=60°，
∵CE⊥AB于E，
∴∠CEB=90°，
∵BC=8cm，
∴CE=BC•sin60°=4$\sqrt{3}$，
∴S平行四边形ABCD=AB•CE=5×4$\sqrt{3}$=20$\sqrt{3}$．
点评 本题考查了平行四边形的性质，平行四边形的面积，三角函数，熟练掌握平行四边形的性质是解题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图，点F、C在BE上，AB∥DE，∠A=∠D，BF=CE，求证：AB=DE．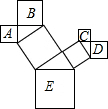
如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、4、2、3，则最大正方形E的面积是38．
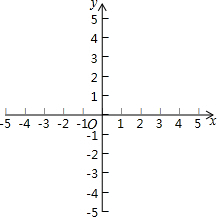我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得，例如，函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到，那么函数y=$\frac{1}{2}$（x-2）2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢？请在图中试一试，你能从中发现什么规律吗？