题目内容
 如图,△ABC中,∠A=40°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于
如图,△ABC中,∠A=40°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:先根据三角形内角和定理求出∠AEF+∠AFE的度数,再由图形翻折变换的性质得出∠AEF=∠DEF,∠AFE=∠DFE,进而可得出结论.
解答:解:∵△AEF中,∠A=40°,
∴∠AEF+∠AFE=180°-40°=140°,
∵△DEF由△AEF翻折而成,
∴∠AEF=∠DEF,∠AFE=∠DFE,
∴∠1+∠2=360°-2(∠AEF+∠AFE)=360°-2×140°=80°.
故答案为:80°.
∴∠AEF+∠AFE=180°-40°=140°,
∵△DEF由△AEF翻折而成,
∴∠AEF=∠DEF,∠AFE=∠DFE,
∴∠1+∠2=360°-2(∠AEF+∠AFE)=360°-2×140°=80°.
故答案为:80°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各式总能成立的是( )
A、
| ||
B、
| ||
C、(
| ||
D、
|
下列调查方式,你认为最合适的是( )
| A、某校招聘教师,对应聘人员面试,采用抽样调查方式 |
| B、了解某型号节能灯的使用寿命,采用普查方式 |
| C、旅客上飞机前的安检,采取抽样调查方式 |
| D、了解某市百岁以上老人的健康情况,采用普查方式 |
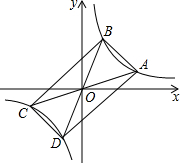 如图,在直角坐标系中,A,B,C,D四点在反比例函数y=
如图,在直角坐标系中,A,B,C,D四点在反比例函数y= 如图,在△ABC中,∠C=90°,AB=10,AC=6,角平分线AE与BF相交于点O,则点O到斜边AB的距离为
如图,在△ABC中,∠C=90°,AB=10,AC=6,角平分线AE与BF相交于点O,则点O到斜边AB的距离为 如图,在梯形ABCD中,AD∥BC,如果∠ABC=60°,BD平分∠ABC,且BD⊥DC,CD=4,那么梯形ABCD的周长是
如图,在梯形ABCD中,AD∥BC,如果∠ABC=60°,BD平分∠ABC,且BD⊥DC,CD=4,那么梯形ABCD的周长是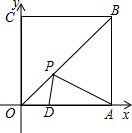 如图,已知四边形OABC为正方形,边长为6,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且点D的坐标为(2,0),点P是OB上的一个动点,则PD+PA的最小值是
如图,已知四边形OABC为正方形,边长为6,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且点D的坐标为(2,0),点P是OB上的一个动点,则PD+PA的最小值是 如图,⊙O的半径为3,点A、B、C在⊙O上,且∠ACB=45°,点O到AB的距离是
如图,⊙O的半径为3,点A、B、C在⊙O上,且∠ACB=45°,点O到AB的距离是