题目内容
 如图,⊙O的半径为3,点A、B、C在⊙O上,且∠ACB=45°,点O到AB的距离是
如图,⊙O的半径为3,点A、B、C在⊙O上,且∠ACB=45°,点O到AB的距离是考点:圆周角定理,等腰直角三角形
专题:
分析:连接OA、OB、作OD⊥AB于点D,证明△OAB是等腰直角三角形,则OD=
AB,据此即可求解.
| 1 |
| 2 |
解答: 解:连接OA、OB、作OD⊥AB于点D.
解:连接OA、OB、作OD⊥AB于点D.
∵△OAB中,OB=OA=3,∠AOB=2∠ACB=90°,
∴AB=
=3
,
又∵OD⊥AB于点D,
∴OD=
AB=
.
故答案是:
.
 解:连接OA、OB、作OD⊥AB于点D.
解:连接OA、OB、作OD⊥AB于点D.∵△OAB中,OB=OA=3,∠AOB=2∠ACB=90°,
∴AB=
| OA2+OB2 |
| 2 |
又∵OD⊥AB于点D,
∴OD=
| 1 |
| 2 |
3
| ||
| 2 |
故答案是:
3
| ||
| 2 |
点评:本题考查了圆周角定理,正确证明△OAB是等腰直角三角形是关键.

练习册系列答案
相关题目
已知两数x,y之和是10,x比y的3倍大2,则下面所列方程组正确的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列说法错误的是( )
| A、对顶角相等 |
| B、两直线平行,内错角相等 |
| C、若∠1+∠2=180°,∠2+∠3=180°,则∠1=∠3 |
| D、两直线被第三条直线所截,同位角相等 |
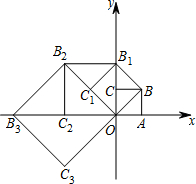 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B2的坐标为
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B2的坐标为 如图,在?ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F=
如图,在?ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F= 如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为
如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为 如图,△ABC中,∠A=40°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于
如图,△ABC中,∠A=40°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于