题目内容
16. 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动2m(即BD=2m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长.
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动2m(即BD=2m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长.
分析 设梯子的长为xm.在Rt△ABO中,根据三角函数得到OB,在Rt△CDO中,根据三角函数得到OD,再根据BD=OD-OB,得到关于x的方程,解方程即可求解
解答 解:解设OB=x,则OD=x+2,
∵∠OBA=60°,
∴cos∠OBA=$\frac{OB}{AB}=\frac{1}{2}$,
∴AB=2x,
∵∠ODA=45°,
∴cos∠ODA=$\frac{OD}{CD}=\frac{{\sqrt{2}}}{2}$,
∴CD=$\sqrt{2}(x+2)$,
∵AB=CD,即2x=$\sqrt{2}(x+2)$,
∴x=$2\sqrt{2}+2$,
∴梯子的长AB=$4\sqrt{2}+4$.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.一书的页码是连续自然数1,2,3,4,5,…规定:前30页不加进去,当从第31页开始,将页码加起来的时候,某个页码加了两次,得出的结果是2015,则这个被加了两次的页码是( )
| A. | 67 | B. | 65 | C. | 63 | D. | 61 |
11.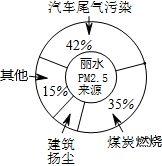 如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
 如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )| A. | 汽车尾气约为建筑扬尘的3倍 | B. | 表示建筑扬尘的占7% | ||
| C. | 表示煤炭燃烧的圆心角约126° | D. | 煤炭燃烧的影响最大 |

