题目内容
1.已知关于x的方程ax+b=0(a≠0)的解为x=-2,点(1,3)是抛物线y=ax2+bx+c(a≠0)上的一个点,则下列四个点中一定在该抛物线上的是( )| A. | (2,3) | B. | (0,3) | C. | (-1,3) | D. | (-3,3) |
分析 根据一次方程ax+b=0(a≠0)的解为x=-2得出b=2a,由此即可得出抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,找出点(1,3)关于对称轴对称的点,即可得出结论.
解答 解:∵关于x的方程ax+b=0(a≠0)的解为x=-2,
∴有-2a+b=0,即b=2a.
∴抛物线y=ax2+bx+c(a≠0)的对称轴x=-$\frac{b}{2a}$=-1.
∵点(1,3)是抛物线上的一点,
∴点(-3,3)是抛物线上的一点.
故选D.
点评 本题考查了二次函数图象上点的坐标特征,解题的关键是找出抛物线的对称轴为x=-1.本题属于基础题,难度不大,解决该题型题目时,找出抛物线的对称轴,找出已知点关于对称轴对称的点即可.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为16.
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为16.
 如图,M为正方形ABCD边AB上一点,DN⊥DM交BC的延长线于点N.求证:AM=CN.
如图,M为正方形ABCD边AB上一点,DN⊥DM交BC的延长线于点N.求证:AM=CN. 如图,在矩形ABCD中,点E、F分别在边BC、AD上,连结DE、EF.四边形CDFE沿EF折叠后得到四边形C′D′FE,点D的对称点D′与点B重合.求证:四边形BEDF是菱形.
如图,在矩形ABCD中,点E、F分别在边BC、AD上,连结DE、EF.四边形CDFE沿EF折叠后得到四边形C′D′FE,点D的对称点D′与点B重合.求证:四边形BEDF是菱形.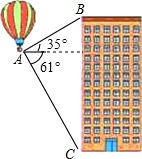 热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)
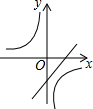
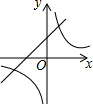
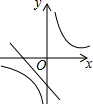
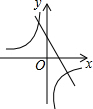
热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)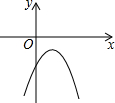 已知二次函数y=-(x-a)2-b的图象如图所示,则反比例函数y=$\frac{ab}{x}$与一次函数y=ax+b的图象可能是( )
已知二次函数y=-(x-a)2-b的图象如图所示,则反比例函数y=$\frac{ab}{x}$与一次函数y=ax+b的图象可能是( )