题目内容
16．
苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥，它的桥拱是抛物线形状，两桥墩的距离是240米，桥拱的拱高60米．（1）求此桥拱的抛物线解析式；
（2）在桥拱上有若干限吊杆垂直拉在桥面上，其中有根吊杆在桥面上的拉点A距桥墩60米处，求此吊杆的长度．
分析 （1）根据题目中的信息，可以设出抛物线的解析式，然后根据题目中的信息即可求得该抛物线的解析式；
（2）将x=60代入第一问求得的抛物线的解析式即可解答本题．
解答 解：（1）设此桥拱的抛物线解析式为：y=a（x-120）2+60
∵点（0，0）在此函数所在的图象上，
∴0=a×（0-120）2+60，
解得a=$-\frac{1}{240}$．
即此桥拱的抛物线的解析式是：y=$-\frac{1}{240}（x-120）^{2}+60$；
（2）将x=60代入y=$-\frac{1}{240}（x-120）^{2}+60$，得
y=45．
即吊杆在桥面上的拉点A距桥墩60米处，则此吊杆的长度是45米．
点评 本题考查二次函数的应用，解题的关键是将该抛物线与二次函数结合在一起，选择合适的平面直角坐标系，设出顶点式，求出抛物线的解析式．
练习册系列答案
相关题目
4．小敏到距家1500米的学校去上学，小敏出发10分钟后，小敏的爸爸立即去追小敏，且在距离学校60米的地方追上了她．已知爸爸比小敏的速度快100米/分，求小敏的速度．若设小敏的速度为x米/分，则根据题意所列方程正确的是（ ）
| A． | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B． | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C． | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D． | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
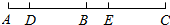如图，线段AC上依次有D，B，E三点，其中点B为线段AC的中点，AD=BE=$\frac{1}{5}$AE，若DB=12．
如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE．