题目内容
17.计算下列各题:(1)$\frac{3c}{16a}$÷$\frac{bc}{2{a}^{2}}$;
(2)$\frac{{x}^{2}+2xy+{y}^{2}}{xy-{y}^{2}}$•$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}+xy}$;
(3)$\frac{x+2y}{{x}^{2}-{y}^{2}}+\frac{y}{{y}^{2}-{x}^{2}}-\frac{2x}{{x}^{2}-{y}^{2}}$;
(4)$\frac{{a}^{2}-{b}^{2}}{a-b}$÷(2+$\frac{{a}^{2}+{b}^{2}}{ab}$).
分析 (1)首先转化为乘法,然后进行约分;
(2)首先把分母和分子分解因式,然后进行约分即可;
(3)利用同分母的分式的加减法进行计算即可;
(4)首先把分母和分子分解因式,计算括号内的式子,然后转化为乘法,进行乘法运算.
解答 解:(1)原式=$\frac{3c}{16a}$•$\frac{2{a}^{2}}{bc}$=$\frac{3a}{6b}$;
(2)原式=$\frac{(x+y)^{2}}{x(x-y)}$•$\frac{(x-y)^{2}}{x(x+y)}$=$\frac{(x+y)(x-y)}{{x}^{2}}$;
(3)原式=$\frac{x+2y}{{x}^{2}-{y}^{2}}$+$\frac{-y}{{x}^{2}-{y}^{2}}$-$\frac{2x}{{x}^{2}-{y}^{2}}$=$\frac{x+2y-y-2x}{(x+y)(x-y)}$=$\frac{y-x}{(x+y)(x-y)}$=-$\frac{1}{x+y}$;
(4)原式=$\frac{(a-b)(a+b)}{a-b}$÷$\frac{(a+b)^{2}}{ab}$=(a+b)•$\frac{ab}{(a+{b)}^{2}}$=$\frac{ab}{a+b}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
5.$\sqrt{(-4)^{2}}$的平方根与$\sqrt{(-2)^{2}}$的和的绝对值是( )
| A. | 0 | B. | 4 | C. | 0或2 | D. | 4或0 |
12.铁道口的栏杆AB的短臂长1.6m,长臂长24m,要想使长臂端点B升高12m,则需要使短臂端点A下降( )
| A. | 0.5m | B. | 0.7m | C. | 1.6m | D. | 0.8m |
2.若一元二次方程3x2-mx+8=0的一个根为2,则m的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 无法确定 |
9.若A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x-6的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
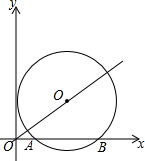 在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=$\frac{4}{5}$x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.
在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=$\frac{4}{5}$x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.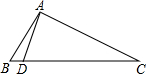 如图,在△ABC中,∠B=2∠C,点D在BC边上,且AD⊥AC,求证:CD=2AB.
如图,在△ABC中,∠B=2∠C,点D在BC边上,且AD⊥AC,求证:CD=2AB.