题目内容
20.(1)计算:(π-2016)0+|1-$\sqrt{2}$|+2-1-2sin45°;(2)解方程:$\frac{2}{2x-1}$=$\frac{4}{4{x}^{2}-1}$;
(3)解不等式组$\left\{\begin{array}{l}{2x-6<6-2x}\\{2x+1>\frac{3+x}{2}}\end{array}\right.$,并写出它的整数解.
分析 (1)原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)分别求出不等式组中两不等式的解集,找出两解集的公共部分求出解集,进而求出整数解即可.
解答 解:(1)原式=1+$\sqrt{2}$-1+$\frac{1}{2}$-$\sqrt{2}$=$\frac{1}{2}$;
(2)去分母得:4x+2=4,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是增根,分式方程无解;
(3)$\left\{\begin{array}{l}{2x-6<6-2x①}\\{2x+1>\frac{3+x}{2}②}\end{array}\right.$,
由①得:x<3,
由②得:x>$\frac{1}{3}$,
∴不等式组的解为$\frac{1}{3}$<x<3,
则它的整数解为:1,2.
点评 此题考查了解分式方程,实数的运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列说法中正确的是( )
| A. | 8的立方根是±2 | |
| B. | $\sqrt{8}$是一个最简二次根式 | |
| C. | 函数y=$\frac{1}{x-1}$的自变量x的取值范围是x>1 | |
| D. | 在平面直角坐标系中,点P(2,3)与点Q(-2,3)关于y轴对称 |
8.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x-y=4}\\{xy=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=2}\\{x+y=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-2y=4}\\{x=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-\frac{3}{3}y=2}\\{2y=x}\end{array}\right.$ |
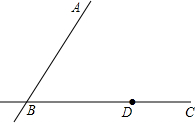 已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点,用尺规作图作出直线DE∥AB.(不写作法,保留作图痕迹)
已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点,用尺规作图作出直线DE∥AB.(不写作法,保留作图痕迹)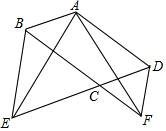 如图,在?ABCD中,∠BCD=120°,分别以BC和CD为边作等边△BCE和等边△CDF.
如图,在?ABCD中,∠BCD=120°,分别以BC和CD为边作等边△BCE和等边△CDF.