题目内容
 如图,等边△ABC的边长为10,BD⊥AC于点D,点M在AB上,AM=4,在BD上找一点P,使PN+PA最小,求这个最小值.
如图,等边△ABC的边长为10,BD⊥AC于点D,点M在AB上,AM=4,在BD上找一点P,使PN+PA最小,求这个最小值.考点:轴对称-最短路线问题,等边三角形的性质
专题:
分析:根据等边三角形的性质求得A、C关于BD对称,从而求得PA=PC,进而得出PA+PM=PC+PM=CM,根据两点之间线段最短,可知CE就是PM+PA最小值,作CQ⊥AB于Q,得出AQ=
AB=5,CQ=5
,最后根据勾股定理即可求得CM.
| 1 |
| 2 |
| 3 |
解答: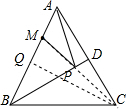 解:连接CM,交BD于P,
解:连接CM,交BD于P,
∵在等边△ABC中,BD⊥AC,
∴BD是AC的垂直平分线,
∴A、C关于BD对称,
∴PA=PC,
∴PA+PM=PC+PM=CM,
根据两点之间线段最短,可知CE就是PM+PA最小值,
作CQ⊥AB于Q,
∴AQ=
AB=5,CQ=5
,
∵AM=4,
∴MQ=5-4=1,
∴CM=
=2
,
∴PM+PA最小值为2
.
 解:连接CM,交BD于P,
解:连接CM,交BD于P,∵在等边△ABC中,BD⊥AC,
∴BD是AC的垂直平分线,
∴A、C关于BD对称,
∴PA=PC,
∴PA+PM=PC+PM=CM,
根据两点之间线段最短,可知CE就是PM+PA最小值,
作CQ⊥AB于Q,
∴AQ=
| 1 |
| 2 |
| 3 |
∵AM=4,
∴MQ=5-4=1,
∴CM=
| MQ2+CQ2 |
| 19 |
∴PM+PA最小值为2
| 19 |
点评:此题主要考查了等边三角形的性质和轴对称及勾股定理等知识的综合应用.根据已知得出两点之间线段最短可得CE就是AP+PE的最小值是解题关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
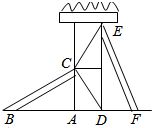 如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )
如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )| A、32° | B、28° |
| C、58° | D、45° |
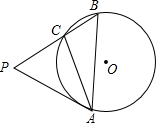 如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.
如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P. 已知AD,AF分别是△ABC的高和角平分线,且∠B=30°,∠C=56°
已知AD,AF分别是△ABC的高和角平分线,且∠B=30°,∠C=56°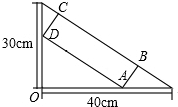 在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上. 如图,在Rt△ABC中,∠C=90°,∠ABC=40°,将△ABC绕点A顺时针旋转α得到△ADE(0°<α<90°)连接CE交AB于点F.
如图,在Rt△ABC中,∠C=90°,∠ABC=40°,将△ABC绕点A顺时针旋转α得到△ADE(0°<α<90°)连接CE交AB于点F. 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF.
如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF. 如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题:
如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题: