题目内容
 (1)⊙O的直径为11cm,若圆心到一直线的距离为5.5cm,那么这条直线和圆的关系是
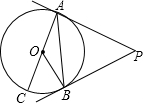
(1)⊙O的直径为11cm,若圆心到一直线的距离为5.5cm,那么这条直线和圆的关系是(2)如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35°,则∠P的度数是
考点:切线的判定,切线的性质
专题:
分析:(1)直接根据直线与圆的位置关系进行解答即可;
(2)根据切线长定理得等腰△PAB,运用内角和定理求解即可.
(2)根据切线长定理得等腰△PAB,运用内角和定理求解即可.
解答:解:(1)∵⊙O的直径为11cm,圆心O到一条直线的距离为5.5cm,
∴直线与圆相切;
(2)根据切线的性质定理得∠PAC=90°,
∴∠PAB=90°-∠BAC=90°-35°=55°.
根据切线长定理得PA=PB,
所以∠PBA=∠PAB=55°,
所以∠P=70°.
故答案为:相切,70°.
∴直线与圆相切;
(2)根据切线的性质定理得∠PAC=90°,
∴∠PAB=90°-∠BAC=90°-35°=55°.
根据切线长定理得PA=PB,
所以∠PBA=∠PAB=55°,
所以∠P=70°.
故答案为:相切,70°.
点评:本题考查的是直线与圆的位置关系,切线的性质定理和切线长定理的应用,熟知设⊙O的半径为r,圆心O到直线l的距离为d,当d=r时,直线l和⊙O相切是解答此题的关键.

练习册系列答案
相关题目
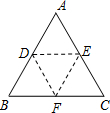 如图,折叠三角形纸片ABC,使点A落在BC边上的点F处,且折痕DE∥BC.若∠C=46°,则∠CFE=( )
如图,折叠三角形纸片ABC,使点A落在BC边上的点F处,且折痕DE∥BC.若∠C=46°,则∠CFE=( )| A、43° | B、44° |
| C、45° | D、46° |
 已知直线a∥b,填空:图(1)中∠1=
已知直线a∥b,填空:图(1)中∠1= 如图所示,求半径为2的圆内接正方形的边心距与面积.
如图所示,求半径为2的圆内接正方形的边心距与面积.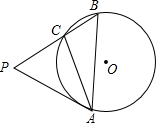 如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.
如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.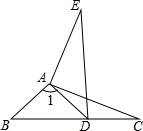 如图,若△ABC≌△ADE,且∠B=38°,则∠1=
如图,若△ABC≌△ADE,且∠B=38°,则∠1= 如图,在Rt△ABC中,∠C=90°,∠ABC=40°,将△ABC绕点A顺时针旋转α得到△ADE(0°<α<90°)连接CE交AB于点F.
如图,在Rt△ABC中,∠C=90°,∠ABC=40°,将△ABC绕点A顺时针旋转α得到△ADE(0°<α<90°)连接CE交AB于点F.