题目内容
9.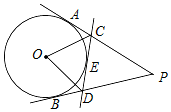 如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点.如∠APB=40°,则∠COD的度数为70°.
如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点.如∠APB=40°,则∠COD的度数为70°.
分析 连接OA、OB、OE,由切线的性质可求出∠AOB,再由切线长定理可得出∠COD=$\frac{1}{2}$∠AOB,可求得答案.
解答  解:
解:
如图,连接OA、OB、OE,
∵PA、PB分别为⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°-∠APB=140°,
∵CD为⊙O的切线,
∴∠AOC=∠EOC,∠BOD=∠DOE,
∴∠COD=∠COE+∠EOD=$\frac{1}{2}$(∠AOE+∠BOE)=$\frac{1}{2}$∠AOB=70°,
故答案为:70°.
点评 本题考查了切线的性质定理以及勾股定理等知识,正确应用切线长定理是解题关键.

练习册系列答案
相关题目
17.由y=x2平移得到抛物线y=(x+1)2-2,则下列平移过程正确的是( )
| A. | 先向左平移1个单位,再向上平移2个单位 | |
| B. | 先向左平移1个单位,再向下平移2个单位 | |
| C. | 先向右平移1个单位,再向下平移2个单位 | |
| D. | 先向右平移1个单位,再向上平移2个单位 |
14.下列计算错误的是( )
| A. | x2•x2=2x4 | B. | (-2a)3=-8a3 | C. | (-a3)2=a6 | D. | (a3)2=a6 |
18.若x:y=5:2,则(x+y):y的值是( )
| A. | 2:5 | B. | 7:2 | C. | 2:7 | D. | 3:2 |
19.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角等于( )
| A. | 160° | B. | 150° | C. | 120° | D. | 60° |
 已知扇形的圆心角为120°,半径6cm,则扇形的弧长为4πcm,扇形的面积为12πcm2.
已知扇形的圆心角为120°,半径6cm,则扇形的弧长为4πcm,扇形的面积为12πcm2.