题目内容
5. 如图,在⊙O中,AB、DE为直径,AB=24,点C在⊙O上,CO⊥AB,OA2+AC2=AD2,则∠ODB所对的弧长等于8π.
如图,在⊙O中,AB、DE为直径,AB=24,点C在⊙O上,CO⊥AB,OA2+AC2=AD2,则∠ODB所对的弧长等于8π.
分析 根据圆周角定理得出∠ADB=90°,根据勾股定理得出3OA2=AD2,AD2+BD2=(2OA)2,进而得出OA=BD,证得∠BOE=120°,根据弧长公式即可求得.
解答 解:∵CO⊥AB,
∵OA2+OC2=AC2,
∵OA=OC,
∴2OA2=AC2,
∵OA2+AC2=AD2,
∴3OA2=AD2,
∵AB为直径,
∴∠ADB=90°,
∴AD2+BD2=(2OA)2,
∴3OA2+BD=4OA2,
∴OA=BD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴∠BOE=120°,
∴∠ODB所对的弧长等于$\frac{120π×12}{180}$=8π.
故答案为8π.
点评 本题考查了圆周角定理,勾股定理等边三角形的判定和性质,弧长公式等,求得三角形OBD是等边三角形是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
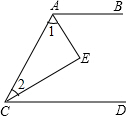 如图所示,根据题意填空已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.
如图所示,根据题意填空已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.
 如图,矩形ABCD中,对角线DB=2AB,若AD=3cm,则矩形ABCD的面积是多少cm2.
如图,矩形ABCD中,对角线DB=2AB,若AD=3cm,则矩形ABCD的面积是多少cm2.