题目内容
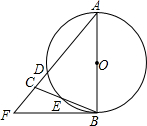 如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质,圆周角定理,解直角三角形
专题:
分析:连接AE,根据AB是直径,得出AE⊥BC,CE=EB,依据已知条件得出∠CBF=∠EAB,FB是圆的且线,进而得出CB的长,然后根据割线定理求得CD的长,最后根据切割线定理求得FC.
解答: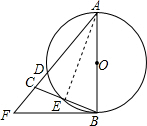 解:连接AE,
解:连接AE,
∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠EAB=
∠CAB,EB=CE=
CB,
∵∠CBF=
∠CAB,tan∠CBF=
,
∴∠CBF=∠EAB,tan∠EAB=
=
,
∴∠CBF+∠ABC=∠EAB+∠ABC=90°,
∴FB是⊙O的切线,
∴FB2=FD•FA,
在RT△AEB中,AB=10,
∴EB=
,
∴CB=2
,CE=
,
∵CE•CB=CD•AC,AC=10,
∴CD=2,
∴AD=AC-CD=8,
设CF=x,则FD=x+2,FA=10+x,FB2=AF2-AB2=(10+x)2-102,
∴(10+x)2-102=(x+2)(10+x),
整理得:x=
,
∴CF=
,
故应选A.
 解:连接AE,
解:连接AE,∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠EAB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠CBF=
| 1 |
| 2 |
| 1 |
| 3 |
∴∠CBF=∠EAB,tan∠EAB=
| EB |
| AE |
| 1 |
| 3 |
∴∠CBF+∠ABC=∠EAB+∠ABC=90°,
∴FB是⊙O的切线,
∴FB2=FD•FA,
在RT△AEB中,AB=10,
∴EB=
| 10 |
∴CB=2
| 10 |
| 10 |
∵CE•CB=CD•AC,AC=10,
∴CD=2,
∴AD=AC-CD=8,
设CF=x,则FD=x+2,FA=10+x,FB2=AF2-AB2=(10+x)2-102,
∴(10+x)2-102=(x+2)(10+x),
整理得:x=
| 5 |
| 2 |
∴CF=
| 5 |
| 2 |
故应选A.
点评:本题考查了圆周角的性质,解直角三角形和勾股定理的应用,切割线定理等,求得FB是圆的切线是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点P(x,y)先向左平移2个单位,再向上平移3个单位得到P′,则点P′的坐标为( )
| A、(x-2,y+3) |
| B、(x+2,y-3) |
| C、(x-3,y+2) |
| D、(x+3,y-2) |
一张试卷有25道题,做对一道题得4分,做错一道题扣1分,一个学生做完全部题目,总得分不低于70分,则他至少要答对( )道题.
| A、16 | B、17 | C、18 | D、19 |
在平面直角坐标系中,点A(2011,-2012)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知
是方程kx+2y=-1的一个解,则k的值是( )
|
A、-
| ||
B、
| ||
C、-
| ||
D、-
|
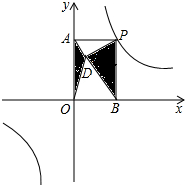 如图,点P是反比例函数y=
如图,点P是反比例函数y=