题目内容
已知实数a、b、c满足a+b+2c=1,a2+b2+6c+
=0,求a、b、c的值.
| 3 |
| 2 |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:首先由a+b+2c=1得出c=-
,再进一步代入a2+b2+6c+
=0,配方求得a、b的数值,进一步求得c的值即可.
| 1-a-b |
| 2 |
| 3 |
| 2 |
解答:解:∵a+b+2c=1,
∴c=-
,
∴a2+b2+6c+
=a2+b2+3-3a-3b+
=(a-
)+(b-
)=0,
∴a=
,b=
,
∴c=-1.
∴c=-
| 1-a-b |
| 2 |
∴a2+b2+6c+
| 3 |
| 2 |
=a2+b2+3-3a-3b+
| 3 |
| 2 |
=(a-
| 3 |
| 2 |
| 3 |
| 2 |
∴a=
| 3 |
| 2 |
| 3 |
| 2 |
∴c=-1.
点评:此题考查配方法的运用,非负数的性质,掌握完全平方公式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了解一批日光灯的合格率,从中抽取了100只日光灯进行检验,则下列说法正确的是( )
| A、这100只日光灯的合格率是总体 |
| B、这一批日光灯的合格率是总体 |
| C、100只日光灯的合格率一定大于这一批日光灯的合格率 |
| D、这种收集数据的方法是全面调查法 |
下列说法正确的是( )
| A、绝对值等于它本身的数是正数和零 |
| B、任何有理数都有倒数 |
| C、立方等于它本身的数只有1和0 |
| D、正整数和负整数统称为整数 |
 已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.当P在AB上运动时,矩形PNDM的最大面积为
已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.当P在AB上运动时,矩形PNDM的最大面积为 如图,是边长为a的正方形剪掉一个边长为b的小正方形,请你用虚线将图形分割后拼成一个长方形,画出图形.
如图,是边长为a的正方形剪掉一个边长为b的小正方形,请你用虚线将图形分割后拼成一个长方形,画出图形.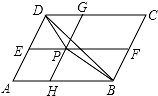 如图,P是平行四边形内一点,过点P分别作AB,AD的平行线,交平行四边形四边形的四边于E、F、G、H,若S四边形PFCG=10,S四边形AHPE=6,则S三角形PBD=
如图,P是平行四边形内一点,过点P分别作AB,AD的平行线,交平行四边形四边形的四边于E、F、G、H,若S四边形PFCG=10,S四边形AHPE=6,则S三角形PBD=