题目内容
 已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.当P在AB上运动时,矩形PNDM的最大面积为
已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.当P在AB上运动时,矩形PNDM的最大面积为考点:正方形的性质,二次函数的最值,矩形的性质
专题:
分析:要求矩形PNDM的面积,应设DN=x,NP=y,则矩形PNDM的面积为S=xy,再结合已知找出y与x的关系,代入后便可求解.
解答:解:设矩形PNDM的边DN=x,NP=y,
则矩形PNDM的面积S=xy(2≤x≤4),
易知CN=4-x,EM=4-y,
且有
=
,
即
=
,
∴y=-
x+5,
S=xy=-
x2+5x(2≤x≤4),
此二次函数的图象开口向下,
对称轴为x=5,
∴当x≤5时,函数值是随x的增大而增大,
对2≤x≤4来说,
当x=4,即PM=4时,S有最大值,
S最大=-
×42+5×4=12,
故答案为:12.
则矩形PNDM的面积S=xy(2≤x≤4),
易知CN=4-x,EM=4-y,
且有
| NP-BC |
| CN |
| BF |
| AF |
即
| y-3 |
| 4-x |
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
S=xy=-
| 1 |
| 2 |
此二次函数的图象开口向下,
对称轴为x=5,
∴当x≤5时,函数值是随x的增大而增大,
对2≤x≤4来说,
当x=4,即PM=4时,S有最大值,
S最大=-
| 1 |
| 2 |
故答案为:12.
点评:本题综合考查了比例线段,二次函数等知识,解此题的关键在于在AB找一点P,转变为求PN和PM的值.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
轮船航行到C处观测小岛A的方向是北偏西54°,那么从A同时观测轮船在C处的方向是( )
| A、南偏东54° |
| B、东偏北36° |
| C、东偏南54° |
| D、南偏东36° |
 如图,一次函数y=-
如图,一次函数y=-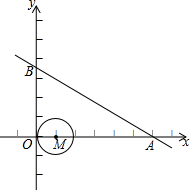 如图,一次函数y=-
如图,一次函数y=- 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OF⊥CD,如果∠AOD=40°.求:
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OF⊥CD,如果∠AOD=40°.求: