题目内容
在梯形ABCD中,AD∥BC,AB=DC=AD=5,CA⊥AB,求BC之长和∠D的度数.
考点:梯形
专题:
分析:根据平行线的性质和等腰三角形的性质推出∠DCB=2∠BCA,根据等腰梯形的性质得出∠B=∠DCB=2∠ACB,求出∠B=60°,∠ACB=30°,根据含30度角的直角三角形的性质求出BC=2AB=10,根据平行线的性质求出∠D即可.
解答: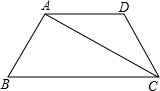 解:∵AD∥BC,
解:∵AD∥BC,
∴∠DAC=∠ACB,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠DCA=∠BCA,
即∠DCB=2∠BCA,
∵在梯形ABCD中,AD∥BC,AB=DC=AD=5,
∴∠B=∠DCB=2∠ACB,
∵CA⊥AB,
∴∠BAC=90°,
∴∠B=60°,∠ACB=30°,
∵AB=5,∠DCB=60°,
∴BC=2AB=10,
∵AD∥BC,
∴∠D=180°-60°=120°.
 解:∵AD∥BC,
解:∵AD∥BC,∴∠DAC=∠ACB,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠DCA=∠BCA,
即∠DCB=2∠BCA,
∵在梯形ABCD中,AD∥BC,AB=DC=AD=5,
∴∠B=∠DCB=2∠ACB,
∵CA⊥AB,
∴∠BAC=90°,
∴∠B=60°,∠ACB=30°,
∵AB=5,∠DCB=60°,
∴BC=2AB=10,
∵AD∥BC,
∴∠D=180°-60°=120°.
点评:本题考查了等腰梯形的性质,平行线的性质,含30度角的直角三角形的性质,等腰三角形的性质的应用,能求出∠ACB=30°是解此题的关键,注意:等腰梯形在同一底上的两个角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
-
的相反数等于( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“实验三角形”,下列各组数据中,能作为一个“实验三角形”三边长的一组是( )
A、1,1,
| ||
B、1,1,
| ||
C、1,2,
| ||
| D、1,2,3 |
 如图,在△ABC中,∠BAC的平分线AB与BC交于点D,线段AD的垂直平分线与线段BC的延长线交于点F.若BD=3,CF=4,则CD=
如图,在△ABC中,∠BAC的平分线AB与BC交于点D,线段AD的垂直平分线与线段BC的延长线交于点F.若BD=3,CF=4,则CD= 如图,已知线段AB和CD的公共部分BD=
如图,已知线段AB和CD的公共部分BD=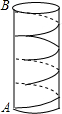 为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为
为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为40,则OH的长等于
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为40,则OH的长等于