题目内容
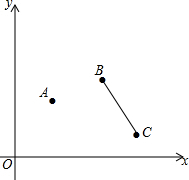 平面直角坐标系中,已知:A(2,3),B(4,4),C(5,1),在x轴上找一点D,使四边形ABCD的周长最小.
平面直角坐标系中,已知:A(2,3),B(4,4),C(5,1),在x轴上找一点D,使四边形ABCD的周长最小.(1)在图中作出D点;
(2)求出D点坐标.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)找点C关于x轴的对称点C′,连接AC′,则AC′与x轴的交点即为点D的位置;
(2)先求出直线AC′的解析式,继而可得出点D的坐标.
(2)先求出直线AC′的解析式,继而可得出点D的坐标.
解答:解:(1)作点C关于x轴的对称点C′,连接AC′,则AC′与x轴的交点即为点D的位置,如图所示:

(2)∵点C坐标为(5,1),
∴C′的坐标为(5,-1)
∵点A坐标为(2,3),
设直线AC′的解析式为y=kx+b,
∴
,
解得
,
∴直线AC′的解析式为:y=-
x+
,
故点D的坐标为(
,0).

(2)∵点C坐标为(5,1),
∴C′的坐标为(5,-1)
∵点A坐标为(2,3),
设直线AC′的解析式为y=kx+b,
∴
|
解得
|
∴直线AC′的解析式为:y=-
| 4 |
| 3 |
| 17 |
| 3 |
故点D的坐标为(
| 17 |
| 4 |
点评:本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.也考查了坐标变换以及待定系数法求一次函数的解析式.

练习册系列答案
相关题目
如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“实验三角形”,下列各组数据中,能作为一个“实验三角形”三边长的一组是( )
A、1,1,
| ||
B、1,1,
| ||
C、1,2,
| ||
| D、1,2,3 |
 如图,钟表上时针与分针所成角的度数是( )
如图,钟表上时针与分针所成角的度数是( )| A、90° | B、100° |
| C、110° | D、120° |
 如图,过矩形ABCD的对角线BD上任意一点O,分别作矩形两边的平行线EF和GH,图中矩形AHOE的面积记为S1,矩形CGOF的面积记为S2,则S1与S2的大小关系为( )
如图,过矩形ABCD的对角线BD上任意一点O,分别作矩形两边的平行线EF和GH,图中矩形AHOE的面积记为S1,矩形CGOF的面积记为S2,则S1与S2的大小关系为( )| A、S1>S2 |
| B、S1<S2 |
| C、S1=S2 |
| D、无法确定 |
 如图,在△ABC中,∠BAC的平分线AB与BC交于点D,线段AD的垂直平分线与线段BC的延长线交于点F.若BD=3,CF=4,则CD=
如图,在△ABC中,∠BAC的平分线AB与BC交于点D,线段AD的垂直平分线与线段BC的延长线交于点F.若BD=3,CF=4,则CD=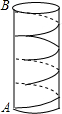 为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为
为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为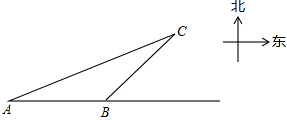 一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?
一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?