题目内容
如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求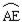 的长.
的长.
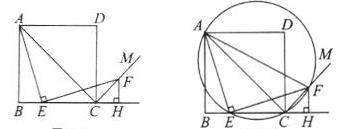
图1 图2
(1)BE=FH ;理由见解析
(2)证明见解析
(3)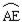 =2π
=2π
【解析】(1)BE=FH。理由如下:
∵四边形ABCD是正方形 ∴∠B=90°,∵FH⊥BC , ∴∠FHE=90°,又∵∠AEF=90°,∴∠AEB+∠HEF=90°, 且∠BAE+∠AEB=90°,∴∠HEF=∠BAE ,∴ ∠AEB=∠EFH ,又∵AE=EF,∴△ABE≌△EHF(SAS),∴BE=FH;
(2)∵△ABE≌△EHF,∴BC=EH,BE=FH , 又∵BE+EC=EC+CH,∴BE=CH,∴CH=FH,∴∠FCH=45°,∴∠FCM=45°,∵AC是正方形对角线,∴ ∠ACD=45°,∴∠ACF=∠FCM +∠ACD =90°;
(3)∵AE=EF,∴△AEF是等腰直角三角形,△AEF外接圆的圆心在斜边AF的中点上。设该中点为O。连结EO得∠AOE=90°
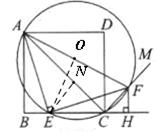
过E作EN⊥AC于点N,Rt△ENC中,EC=4,∠ECA=45°,∴EN=NC=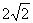 ,Rt△ENA中,EN =
,Rt△ENA中,EN =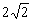 ,又∵∠EAF=45°,∠CAF=∠CEF=15°(等弧对等角),∴∠EAC=30°,∴AE=
,又∵∠EAF=45°,∠CAF=∠CEF=15°(等弧对等角),∴∠EAC=30°,∴AE=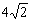 ,Rt△AFE中,AE=
,Rt△AFE中,AE=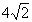 = EF,∴AF=8, AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°,
= EF,∴AF=8, AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°, =2π·4·(90°÷360°)=2π.
=2π·4·(90°÷360°)=2π.

 阅读快车系列答案
阅读快车系列答案 正方形
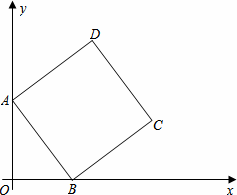
正方形 中,动点
中,动点 分别以相同的速度从
分别以相同的速度从 两点同时出发向
两点同时出发向 和
和 运动(任何一个点到达即停止),在运动过程中,则线段
运动(任何一个点到达即停止),在运动过程中,则线段 的最小值为
的最小值为
 )÷(a﹣2+
)÷(a﹣2+ ),其中,a满足a﹣2=0.
),其中,a满足a﹣2=0.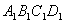 ,算出了它的面积.然后分别取正方形
,算出了它的面积.然后分别取正方形 作出了第二个正方形
作出了第二个正方形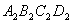 ,算出了它的面积.用同样的方法,作出了
,算出了它的面积.用同样的方法,作出了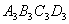 ,算出了它的面积 ,由此可得,第六个正方形
,算出了它的面积 ,由此可得,第六个正方形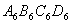 的面积
的面积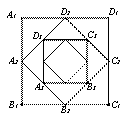
 有意义,则x应满足( )
有意义,则x应满足( ) B.x≤3且
B.x≤3且
 D.
D.