题目内容
已知二次函数的图象与x轴交于点A(1,0),B(3,0),与y轴交于点C(0,3)
(1)求二次函数的解析式
(2)在抛物线的对称轴上确定一点P,使得△ACQ的周长最小,并求出点P的坐标和△ACQ的周长的最小值.
(1) ;(2)P(2,1),
;(2)P(2,1),
 .
.
【解析】(1)设二次函数的解析式为 ,把点A(1,0),B(3,0)代入得
,把点A(1,0),B(3,0)代入得 ,把点C(0,3)代入得a=1,所以二次函数的解析式为
,把点C(0,3)代入得a=1,所以二次函数的解析式为 ;(2)连结BC,直线BC与对称轴的交点即为点P,设直线BC的解析式为
;(2)连结BC,直线BC与对称轴的交点即为点P,设直线BC的解析式为 ,把B(3,0),点C(0,3)代入得
,把B(3,0),点C(0,3)代入得 ,解得
,解得 ,所以直线解析式为
,所以直线解析式为 ,又二次函数的图象与x轴交于点A(1,0),B(3,0),所
,又二次函数的图象与x轴交于点A(1,0),B(3,0),所
以对称轴为 ,把
,把 代入
代入
 得y=1,所以点P的坐标为(2,1),在Rt△BOC和Rt△AOC中,由勾股定理可得:AC=
得y=1,所以点P的坐标为(2,1),在Rt△BOC和Rt△AOC中,由勾股定理可得:AC= ,BC=
,BC= ,所以△ACQ的周长的最小值=AC+BC=
,所以△ACQ的周长的最小值=AC+BC= .
.

练习册系列答案
相关题目

 的解为x= .
的解为x= . 的长.
的长.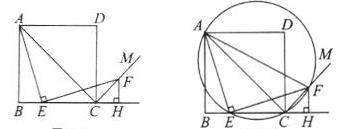
 ,x是不等式2x-3(x-2)≥1的一个非负整数解.
,x是不等式2x-3(x-2)≥1的一个非负整数解.
 的两个根,则a2-5a-b+ab= .
的两个根,则a2-5a-b+ab= . 格点上,则与△ABC相似的三角形所在的网格图形是图 ( ).
格点上,则与△ABC相似的三角形所在的网格图形是图 ( ).
