题目内容
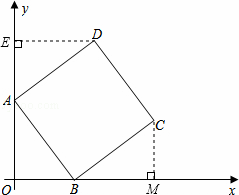
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
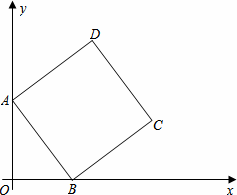
【解析】(1)x2﹣7x+12=0,解得x1=3,x2=4,∵OA>OB,∴OA=4,OB=3,过D作DE⊥y于点E,∵正方形ABCD,∴AD=AB,∠DAB=90°,∠DAE+∠OAB=90°,∠ABO+∠OAB=90°,∴∠ABO=∠DAE,∵DE⊥AE,∴∠AED=90°=∠AOB,∵DE⊥AE∴∠AED=90°=∠AOB,
∴△DAE≌△ABO(AAS),∴DE=OA=4,AE=O B=3,∴OE=7,∴D(4,7);
B=3,∴OE=7,∴D(4,7);
(2)过点C作CM⊥x 轴于点M,
轴于点M,
同上可证得△BCM≌△ABO,∴CM=OB=3,BM=OA=4,∴OM=7,∴C(7,3),
设直线BC的解析式为y=kx+b(k≠0,k、b为常数),代入B(3,0),C(7,3)得, ,
,
解得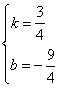 ,∴y=
,∴y=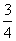 x﹣
x﹣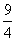 ;
;
(3)存在.
点P与点B重合时,P1(3,0),
点P与点B关于点C对称时,P2(11,6).

练习册系列答案
相关题目
 ,则
,则 .
. 的解为x= .
的解为x= .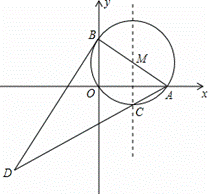

 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论: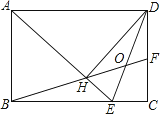
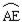 的长.
的长.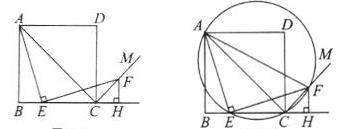
 格点上,则与△ABC相似的三角形所在的网格图形是图 ( ).
格点上,则与△ABC相似的三角形所在的网格图形是图 ( ).
