题目内容
13.已知点A、B的坐标分别为(2,2)、(5,1),试在x轴上找一点C,使△ABC为直角三角形.分析 当△ABC为直角三角形时,设点C坐标为(x,0),分三种情况:①如果A为直角顶点,根据勾股定理列方程求得x的值;②如果B为直角顶点,那么AB2+BC2=AC2根据勾股定理列方程求得x的值③如果C为直角顶点,C为直角顶点这种情况不存在,于是得到结论.
解答 解:当△ABC为直角三角形时,设点C坐标为(x,0),分三种情况:
①如果A为直角顶点,则AB2+AC2=BC2,
即(2-5)2+(2-1)2+(2-x)2+22=(5-x)2+1,
解得:x=$\frac{4}{3}$,
②如果B为直角顶点,那么AB2+BC2=AC2,
即(2-5)2+(2-1)2+(5-x)2+1=(2-x)2+22,
解得x=$\frac{14}{7}$,
③如果C为直角顶点,那么AB2=AC2+BC2,
即(2-5)2+(2-1)2=(2-x)2+22+(5-x)2+1,
解得x=3或4,
综上可知,使△PAB为直角三角形的点C坐标为($\frac{4}{3}$,0)或($\frac{14}{3}$,0)或(3,0)或(4,0).
点评 本题考查了勾股定理,坐标与图形性质,x轴上点的坐标特征,进行分类讨论是解题的关键.

练习册系列答案
相关题目
1.太阳的质量约为2.1×1027t,地球的质量约为6×1021t.则太阳的质量约是地球质量的( )
| A. | 3.5×106倍 | B. | 3.5×105倍 | C. | 3.5×107倍 | D. | 3.5×104倍 |
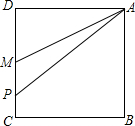 如图,在正方形ABCD的边CD上取一点P,使AP=PC+CB,M是DC的中点.求证:∠MAD=$\frac{1}{2}$∠BAP.
如图,在正方形ABCD的边CD上取一点P,使AP=PC+CB,M是DC的中点.求证:∠MAD=$\frac{1}{2}$∠BAP.