题目内容
2．化简：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）（1-$\frac{1}{{5}^{2}}$）…（1-$\frac{1}{100{3}^{2}}$）（1-$\frac{1}{100{4}^{2}}$）=$\frac{1005}{2008}$．分析 利用平方差公式把每一项因式分解，进一步交错约分得出答案即可．
解答 解：原式=（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1-$\frac{1}{3}$）（1+$\frac{1}{3}$）（1-$\frac{1}{4}$）（1+$\frac{1}{4}$）×…×（1-$\frac{1}{1003}$）（1+$\frac{1}{1003}$）（1-$\frac{1}{1004}$）（1+$\frac{1}{1004}$）
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…××$\frac{1002}{1003}$×$\frac{1004}{1003}$×$\frac{1003}{1004}$×$\frac{1005}{1004}$
=$\frac{1005}{2008}$．
故答案为：$\frac{1005}{2008}$．
点评 此题考查因式分解的运用，掌握平方差公式是解决问题的关键．
练习册系列答案
相关题目
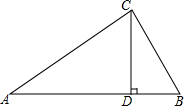如图所示，已知在Rt△ABC中，CD是斜边AB上的高，AC=8，BC=6，求CD的长．