题目内容
5.若a、b为实数,且b=$\frac{\sqrt{{a}^{2}-1}+\sqrt{1-{a}^{2}}}{a+7}$+4,则a+b=5或3.分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出a的值,b的值,根据有理数的加法,可得答案.
解答 解:由被开方数是非负数,得
$\left\{\begin{array}{l}{{a}^{2}-1≥0}\\{1-{a}^{2}≥0}\end{array}\right.$,
解得a=1,或a=-1,b=4,
当a=1时,a+b=1+4=5,
当a=-1时,a+b=-1+4=3,
故答案为:5或3.
点评 本题考查了二次根式有意义的条件,当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
15.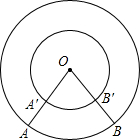 如图,两个同心圆的圆心为点O,A,B是最大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,那么( )
如图,两个同心圆的圆心为点O,A,B是最大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,那么( )
 如图,两个同心圆的圆心为点O,A,B是最大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,那么( )
如图,两个同心圆的圆心为点O,A,B是最大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,那么( )| A. | $\widehat{AB}$=$\widehat{A′B′}$ | B. | $\widehat{AB}$>$\widehat{A′B′}$ | ||
| C. | $\widehat{AB}$的度数等于$\widehat{A′B′}$的度数 | D. | $\widehat{AB}$的长度等于$\widehat{A′B′}$的长度 |
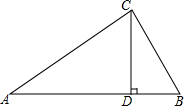 如图所示,已知在Rt△ABC中,CD是斜边AB上的高,AC=8,BC=6,求CD的长.
如图所示,已知在Rt△ABC中,CD是斜边AB上的高,AC=8,BC=6,求CD的长.