题目内容
13.如图,水平地面有一个面积为120πcm2的灰色扇形OAB,其中OA的长度为12cm,且OA与地面垂直.若在没有滑动的情况下,将图最左边的扇形向右滚动至点A 再一次接触地面时,则O点移动的路径长为22π.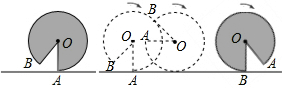
分析 根据题意可知点O移动的距离正好是灰色扇形的弧长,所以先根据扇形的面积求得扇形的圆心角的度数,再根据弧长公式求得弧长,即点O从开始到移动到OB与直线垂直移动的距,然后通过一次旋转,点A再一次接触地面,利用弧长公式即可求得移动的距离.
解答 解:设扇形的圆心角为n,则$\frac{nπ•144}{360}$=120π
∴n=300°
∵扇形的弧长为$\frac{300π•12}{180}$=20π
∴点O从开始到移动到OB与直线垂直,移动的距离10πcm.
∵∠AOB=360-300=60°,
则△AOB是等边三角形,
∴AB=OA=12cm,
则A在图乙中最后一个图形的位置旋转到A与直线接触,O移动的距离是:$\frac{30π×12}{180}$=2π,
则OO点移动了22π.
故答案为:22π.
点评 本题考查了扇形的面积公式和弧长公式,解决本题要牢记扇形的面积公式和弧长公式.要会从题意中分析得到点O移动的路线是关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
3.如果规定“※”为一种运算符号,且a※b=ab-ba,则4※(2※1)的值为 ( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
8. 如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,…,Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3、…、An-1An都在x轴上.A4点的横坐标为( )
如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,…,Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3、…、An-1An都在x轴上.A4点的横坐标为( )
 如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,…,Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3、…、An-1An都在x轴上.A4点的横坐标为( )
如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,…,Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3、…、An-1An都在x轴上.A4点的横坐标为( )| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
18.某种原子的直径是2×10-3纳米,把这个数化为小数是( )纳米.
| A. | 0.002 | B. | -0.002 | C. | 2000 | D. | 200 |
2.下列函数中,图象通过原点的是( )
| A. | y=2x+1 | B. | y=x2-1 | C. | y=3x2 | D. | y=$\frac{1}{{x}^{2}-1}$ |
 已知抛物线y=ax2+bx+3,经过点M(-4,0),且对称轴为x=-$\frac{5}{2}$,交y轴于B.
已知抛物线y=ax2+bx+3,经过点M(-4,0),且对称轴为x=-$\frac{5}{2}$,交y轴于B. 国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:
国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示: 如图,已知线段a,b,且a>b,用直尺和圆规作一条线段,使它等于3a-b.(要求保留作图痕迹,并写出作法)
如图,已知线段a,b,且a>b,用直尺和圆规作一条线段,使它等于3a-b.(要求保留作图痕迹,并写出作法)