题目内容
5.已知(x2+mx+n)(x2-3x+2)的展开式不含x3和x2的项,那么m=3,n=7.分析 根据多项式乘以多项式的法则,可表示为(x2+mx+n)(x2-3x+2)=x4-(3-m)x3+(2+n-3m)x2+(2m-3n)x+2n,再令x3和x2项系数为0,计算即可.
解答 解:(x2+mx+n)(x2-3x+2)=x4-(3-m)x3+(2+n-3m)x2+(2m-3n)x+2n,
∵(x2+mx+n)(x2-3x+2)的展开式中不含x3和x2项,
则有$\left\{\begin{array}{l}{3-m=0}\\{2+n-3m=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=3}\\{n=7}\end{array}\right.$.
故答案为:3,7.
点评 本题主要考查多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14. 如图,晚上小明由甲处径直走到乙处的过程中,他在路灯M下的影长在地面上的变化情况是( )
如图,晚上小明由甲处径直走到乙处的过程中,他在路灯M下的影长在地面上的变化情况是( )
 如图,晚上小明由甲处径直走到乙处的过程中,他在路灯M下的影长在地面上的变化情况是( )
如图,晚上小明由甲处径直走到乙处的过程中,他在路灯M下的影长在地面上的变化情况是( )| A. | 逐渐变短 | B. | 先变短后变长 | C. | 先变长后变短 | D. | 逐渐变长 |
15.下列各数中,是无理数的是( )
| A. | $\sqrt{4}$ | B. | -2 | C. | 0 | D. | -π |
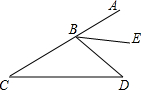 如图,在△BCD中,∠C=30°,∠D=40°,点A为CB的延长线上一点,BE为∠ABD的角平分线,则∠ABE=35°.
如图,在△BCD中,∠C=30°,∠D=40°,点A为CB的延长线上一点,BE为∠ABD的角平分线,则∠ABE=35°.
 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE所叠得△DFE,延长EF交边AB于点G,连接DG,BF,给出以下结论:
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE所叠得△DFE,延长EF交边AB于点G,连接DG,BF,给出以下结论: 如图所示,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,求∠BOC和∠COD的度数.
如图所示,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,求∠BOC和∠COD的度数.