题目内容

15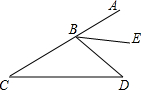．如图，在△BCD中，∠C=30°，∠D=40°，点A为CB的延长线上一点，BE为∠ABD的角平分线，则∠ABE=35°．

分析 由外角性质可得∠ABD的度数，再利用角平分线的定义可得结果．

解答 解：∵∠C=30°，∠D=40°，
∴∠ABD=∠C+∠D=30°+40°=70°，
∵BE为∠ABD的角平分线，
∴$∠ABE=\frac{1}{2}∠ABD=\frac{1}{2}×70°$=35°，
故答案为：35．

点评 本题主要考查了外角的性质和角平分线的定义，利用外角的性质得∠ABD的度数是解答此题的关键．

练习册系列答案
相关题目
20．阅读材料：黑白双雄、纵横江湖；双剑合璧，天下无敌．这是武侠小说中常见的描述，其意是指两人合在一起，取长补短，威力无比．在二次根式中也有这种相辅相成的“对子”如：（2+$\sqrt{3}$）（2-$\sqrt{3}$）=1，2+$\sqrt{3}$与2-$\sqrt{3}$的积不含有根号，我们就说这两个式子互为有理化因式，其中一个是另一个的有理化因式．于是二次根式$\frac{2+\sqrt{3}}{2-\sqrt{3}}$可以这样解：$\frac{2+\sqrt{3}}{2-\sqrt{3}}=\frac{（2+\sqrt{3}）（2+\sqrt{3}）}{（2-\sqrt{3}）（2-\sqrt{3}）}=\frac{7+4\sqrt{3}}{1}=7+4\sqrt{3}$，像这样，通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化．
解决问题：①$4+\sqrt{7}$的有理化因式是4-$\sqrt{7}$
②计算：$\frac{1}{2+\sqrt{3}}+\sqrt{27}-6\sqrt{\frac{1}{3}}$
③计算：$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…$+\frac{1}{\sqrt{2015}+\sqrt{2016}}$．
6．下列各式中的单项式是（　　）
A．-1+xB．-$\frac{x-1}{3}$C．$\frac{-x}{2}$D．2（x+1）
3．已知直线l1：y1=x+m与直线l2：y2=nx+3相交于点A（1，2）．
（1）求m、n的值；
（2）设l1交x轴于点B，l2交x轴于点C，若点D与点A，B，C能构成平行四边形，请直接写出D点坐标；
（3）请在所给坐标系中画出直线l1和l2，并根据图象回答问题：
当x满足x＞1时，y1＞2；
当x满足0≤x＜3时，0＜y2≤3；
当x满足x＜1时，y1＜y2．
10．某地区居民生活用电基本价格为每千瓦时0.50元，若每月用电量超过a千瓦则超过部分按基本电价的80%收费．
（1）某户八月份用电96千瓦时，共交电费46.4元，求a．
（2）若该用户九月份的平均电费为0.48元，则九月份共用电多少千瓦？应交电费多少元？
20．如图所示四幅图中，符合“射线PA与射线PB是同一条射线”的图为（　　）
A．B．C．D．
7．如图，画图并填空：
（1）画直线AB；
（2）连接DC，并延长交AB于P；
（3）画射线DA；
（4）在平面内找一点O，使OA+OB+OC+OD最小；
（5）在所画出的图形中，线段共13条；若点C在点A的北偏东60°方向，则点O在点C的南偏西60°方向．
4．在下列单项式中，不是同类项的是（　　）
A．-2x2y和-yx2B．-3和0C．-a2bc和ab2cD．-mnt和-8mnt
5．已知（x2+mx+n）（x2-3x+2）的展开式不含x3和x2的项，那么m=3，n=7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网