题目内容
16.(1)计算:2013×2015-2014×2014;(2)计算:${(-\frac{1}{3}xy}^{2})^{2}$-[xy(2x-y)+xy2];
(3)分解因式:a2(x-y)+b2(y-x);
(4)解不等式:(x+3)(x-7)+8>(x+5)(x-1);
(5)解方程:(3x+2)(3x-2)=(9x+5)(x-2)+15;
(6)分解因式:3xy4-24xy2+48x.
分析 (1)把2013×2015=(2014-1)×(2014+1)利用平方差公式展开计算即可;
(2)按照积的乘方,整式的乘法计算,进一步去括号合并得出答案即可;
(3)利用提取公因式法和平方差公式因式分解即可;
(4)利用不等式的性质求得不等式的解集即可;
(5)先利用平方差公式和整式的乘法化简方程,进一步求得方程的解即可;
(6)利用提取公因式法和完全平方公式因式分解即可.
解答 解:(1)原式=(2014-1)×(2014+1)-2014×2014
=2014×2014-1-2014×2014
=-1;
(2)原式=$\frac{1}{9}$x2y4-[2x2y-xy2+xy2]
=$\frac{1}{9}$x2y4-2x2y;
(3)原式=(a2-b2)(x-y)
=(a+b)(a-b)(x-y);
(4)(x+3)(x-7)+8>(x+5)(x-1)
x2-4x-21>x2+4x-5
-8x>16
x<-2;
(5)(3x+2)(3x-2)=(9x+5)(x-2)+15
9x2-4=9x2-13x-10+15
13x=9
x=$\frac{9}{13}$;
(6)原式=3x(y4-8y2+16)
=3x(y2-4)2
=3x(y+2)2(y-2)2.
点评 此题考查整式的混合运算,解不等式,解一元一次方程,因式分解,掌握计算方法,计算公式以及解答的步骤与方法是解决问题的关键.

练习册系列答案
相关题目
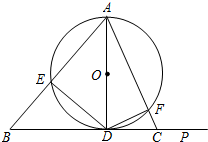 如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF.
如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF. 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:∠ABE=∠ACE.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:∠ABE=∠ACE.