题目内容
4.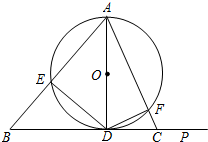 如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF.
如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF.(1)求∠EDF的度数;
(2)已知P是射线DC上一个动点,当点P运动到PD=BD时,连结AP,交⊙O于G,连结DG.若∠BAC=70°,∠APB=50°,⊙O 的半径长为1,
①求证:∠EDG+∠BAG=180°;
②求劣弧DF的长.
分析 (1)如图,直接运用圆内接四边形的性质,求出∠EDF,即可解决问题.
(2)如图,作辅助线;要求劣弧DF的长,需求出圆心角∠DOF的度数;因此,只要求出∠DAC;首先证明AB=AP,得到∠B=∠APD=50°;根据直角三角形的两锐角互余求出∠BAD,进而求出∠DAC;运用弧长公式即可解决问题.
解答 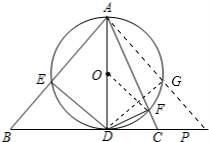 解:(1)如图,设∠BAC=α;
解:(1)如图,设∠BAC=α;
∵四边形AEDF为⊙O的内接四边形,
∴∠EDF+∠EAF=180°,
∴∠EDF=180°-α.
(2)①如图,∵四边形AEDG是⊙O的内接四边形,
∴∠EDG+∠BAG=180°.
②如图,连接OF;
∵AD⊥BP,BD=PD,
∴AD为线段BP的垂直平分线,
∴AB=AP,∠B=∠APB=50°,
∴∠BAD=90°-50°=40°,而∠BAC=70°,
∴∠DAC=30°,∠DOF=60°,
∴$\widehat{DF}$的长=$\frac{60π•1}{180}$=$\frac{π}{3}$.
点评 该题以圆为载体,以考查圆内接四边形的性质、线段垂直平分线的性质、圆周角定理、弧长公式及其应用等几何知识点为核心构造而成;牢固掌握圆内接四边形的性质、线段垂直平分线的性质、圆周角定理等是基础,灵活运用是关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目