题目内容
已知:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;…则1+3+5+…+99=________;
502
分析:观察题目中的式子.可以得到一个规律,等号左边有几个奇数,等号右边的数就是几的平方,再观察分析1+3+5+…+99找出规律求出共有多少个奇数,进而求解.
解答:由1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;…得到:
1是1个奇数等于12,1+3是2个奇数等于22,1+3+5是3个奇数等于32,1+3+5+7是4个奇数等于42,…
由此1+3+5+…+99,算出由几个奇数就等于几的平方.
1+3+5+…+99是由1,3,5,…,99.是首项为1,公差为2的等差数列,
设共有n项,则:
99=1+2(n-1),
得n=50.
故答案为:502.
点评:此题考查的知识点是数字的变化类,其关键是找出所有等式的规律和组成1+3+5+…+99的数的规律.
分析:观察题目中的式子.可以得到一个规律,等号左边有几个奇数,等号右边的数就是几的平方,再观察分析1+3+5+…+99找出规律求出共有多少个奇数,进而求解.
解答:由1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;…得到:
1是1个奇数等于12,1+3是2个奇数等于22,1+3+5是3个奇数等于32,1+3+5+7是4个奇数等于42,…
由此1+3+5+…+99,算出由几个奇数就等于几的平方.
1+3+5+…+99是由1,3,5,…,99.是首项为1,公差为2的等差数列,
设共有n项,则:
99=1+2(n-1),
得n=50.
故答案为:502.
点评:此题考查的知识点是数字的变化类,其关键是找出所有等式的规律和组成1+3+5+…+99的数的规律.

练习册系列答案
相关题目
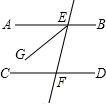 如图,AB∥CD,EG平分∠AEF,∠DFE=70°,求∠GEF的度数.
如图,AB∥CD,EG平分∠AEF,∠DFE=70°,求∠GEF的度数.