题目内容
16.某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
分析 (1)每天的销售利润W=每天的销售量×每件产品的利润;
(2)根据配方法,可得答案;
(3)根据自变量与函数值的对应关系,可得答案.
解答 解:(1)w=(x-30)•y=(-x+60)(x-30)=-x2+30x+60x-1800=-x2+90x-1800,
w与x之间的函数解析式w=-x2+90x-1800;
(2)根据题意得:w=-x2+90x-1800=-(x-45)2+225,
∵-1<0,
当x=45时,w有最大值,最大值是225.
(3)当w=200时,-x2+90x-1800=200,解得x1=40,x2=50,
∵50>48,x2=50不符合题意,舍,
答:该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为40元.
点评 本题考查了二次函数的应用;得到每天的销售利润的关系式是解决本题的关键;利用配方法或公式法求得二次函数的最值问题是常用的解题方法.

练习册系列答案
相关题目
6.下列函数中,对于任意实数x1,x2,当x1>x2时,满足y1<y2的是( )
| A. | y=-3x+2 | B. | y=2x+1 | C. | y=2x2+1 | D. | y=-$\frac{1}{x}$ |
4.单项式9xmy3与单项式4x2yn是同类项,则m+n的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.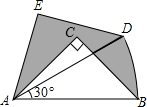 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
1.计算x6÷x2正确的是( )
| A. | 3 | B. | x3 | C. | x4 | D. | x8 |
8.下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )


| A. | 73 | B. | 81 | C. | 91 | D. | 109 |
5.下列图标中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
