题目内容
4.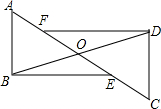 如图,△ABO≌△CDO,点E、F在线段AC上,FD∥EB,求证:FD=EB.
如图,△ABO≌△CDO,点E、F在线段AC上,FD∥EB,求证:FD=EB.
分析 先根据全等三角形的性质,由△ABO≌△CDO得到OB=OD,再根据平行线的性质由DF∥EB得到∠OBE=∠ODF,则可根据“ASA”判断△BOE≌△DOF,所以FD=EB.
解答 证明:∵△ABO≌△CDO,
∴OB=OD,
∵DF∥EB,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠OBE=∠ODF}\\{OB=OD}\\{∠BOE=∠DOF}\end{array}\right.$,
∴△BOE≌△DOF,
∴FD=EB.
点评 本题考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等;全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
16.估计$\sqrt{50}$的大小应在( )
| A. | 7.0至7.5之间 | B. | 7.5至8.0之间 | C. | 8.0至8.5之间 | D. | 8.5至9.0之间 |
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点B开始沿AB边向点A以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从B同时出发,问几秒钟时△DPQ的面积等于12cm2?
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点B开始沿AB边向点A以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从B同时出发,问几秒钟时△DPQ的面积等于12cm2?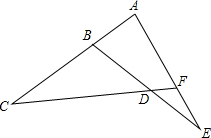 如图,∠C=30°,∠E=28°,∠BDF=130°,求∠A与∠EFD的度数.
如图,∠C=30°,∠E=28°,∠BDF=130°,求∠A与∠EFD的度数. 如图,ABCD和DEFG都是正方形,请问:三角形ADG与三角形CDE的面积之比是多少?
如图,ABCD和DEFG都是正方形,请问:三角形ADG与三角形CDE的面积之比是多少?