题目内容
19.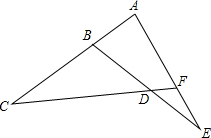 如图,∠C=30°,∠E=28°,∠BDF=130°,求∠A与∠EFD的度数.
如图,∠C=30°,∠E=28°,∠BDF=130°,求∠A与∠EFD的度数.
分析 先根据邻补角求得∠EDF=50°,进而根据三角形内角和定理求得∠EFD的度数,根据三角形外角的性质求得∠AFC的度数,然后根据三角形内角和定理即可求得∠A的度数.
解答 解:∵∠BDF=130°,
∴∠EDF=180°-130°=50°,
∵∠E=28°,
∴∠AFC=∠EDF+∠E=50°+28°=78°,
∴∠EFD=180°-78°=102°,
∵∠C=30°,
∴∠A=180°-∠C-∠AFC=180°-30°-78°=72°.
点评 本题考查了三角形内角和等于和三角形外角的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
9.下列各数+(-4),-(+$\frac{1}{4}$),-[+(-$\frac{1}{4}$)],+[-(+$\frac{1}{4}$)],+[-(-4)]中,正数有( )
| A. | 0个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列式子成立的是( )
| A. | xy2-2y2•x=-xy2 | B. | 3a+5b=8ab | C. | 3ab-ab=2 | D. | a3•a2=a6 |
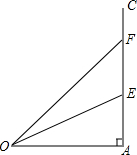 已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.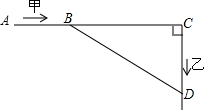 如图,东西方向上有A,C两地相距10km,甲以16km/h的速度从A地出发向正东方向前进,乙以12km/h的速度从C地出发向正南方向前进,问:最快经过多少小时,甲、乙两人相距6km?
如图,东西方向上有A,C两地相距10km,甲以16km/h的速度从A地出发向正东方向前进,乙以12km/h的速度从C地出发向正南方向前进,问:最快经过多少小时,甲、乙两人相距6km?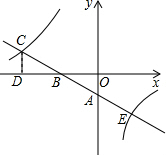 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=$\frac{m}{x}$的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若0B=2、0D=4,△A0B的面积为1.
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=$\frac{m}{x}$的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若0B=2、0D=4,△A0B的面积为1.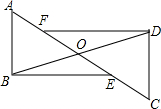 如图,△ABO≌△CDO,点E、F在线段AC上,FD∥EB,求证:FD=EB.
如图,△ABO≌△CDO,点E、F在线段AC上,FD∥EB,求证:FD=EB.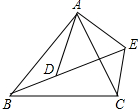 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.