题目内容
14. 如图,ABCD和DEFG都是正方形,请问:三角形ADG与三角形CDE的面积之比是多少?
如图,ABCD和DEFG都是正方形,请问:三角形ADG与三角形CDE的面积之比是多少?
分析 由正方形的性质得出∠ADC=∠GDE=90°,AD=CD,DG=DE,得出∠ADG+∠CDE=180°,由三角函数关系得出sin∠ADG=sin∠CDE,又S△ADG=$\frac{1}{2}$AD•DG•sin∠ADG,S△CDE=$\frac{1}{2}$CD•DE•sin∠CDE,得出S△ADG=S△CDE,即可得出结论.
解答 解:三角形ADG与三角形CDE的面积之比是1;理由如下:
∵四边形ABCD和四边形DEFG都是正方形,
∴∠ADC=∠GDE=90°,AD=CD,DG=DE,
∴∠ADG+∠CDE=180°,
∴sin∠ADG=sin∠CDE,
∴S△ADG=$\frac{1}{2}$AD•DG•sin∠ADG,S△CDE=$\frac{1}{2}$CD•DE•sin∠CDE,
∴S△ADG=S△CDE,
∴三角形ADG与三角形CDE的面积之比是1.
点评 本题考查了正方形的性质、三角函数、三角形面积的计算方法;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
2.在同一坐标系中,抛物线y=x2,y=-x2的共同性质是( )
| A. | 关于y轴对称,开口向上 | B. | 关于y轴对称,顶点坐标为(0,0) | ||
| C. | 关于x轴对称,开口向下 | D. | 关于x轴对称,都有最高点 |
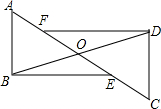 如图,△ABO≌△CDO,点E、F在线段AC上,FD∥EB,求证:FD=EB.
如图,△ABO≌△CDO,点E、F在线段AC上,FD∥EB,求证:FD=EB. 如图,在△ABC中,∠ACB=90°,点D、E分别为AC、AB的中点,延长BC到F使$CF=\frac{1}{2}BC$.
如图,在△ABC中,∠ACB=90°,点D、E分别为AC、AB的中点,延长BC到F使$CF=\frac{1}{2}BC$.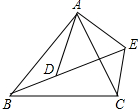 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$. 把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.
把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.