题目内容
20.若不等式组$\left\{\begin{array}{l}{3+x>2m}\\{2x-m≤0}\end{array}\right.$有解,则m的取值范围是m<2.分析 分别求出每一个不等式的解集,结合题意根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定关于m的不等式组,解不等式组可得.
解答 解:解不等式3+x>2m,得:x>2m-3,
解不等式2x-m≤0,得:x≤$\frac{m}{2}$,
∵不等式组有解,
∴$\frac{m}{2}$>2m-3,
解得:m<2,
故答案为:m<2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.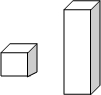 图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )
图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )
 图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )
图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是( )| A. | 主视图相同 | B. | 俯视图相同 | ||
| C. | 左视图相同 | D. | 主视图、俯视图、左视图都相同 |
15.若a>b,且c为实数,有下列各式:
①ac>bc;②ac<bc;③ac2>bc2;④ac2≥bc2;⑤$\frac{a}{c}$>$\frac{b}{c}$
其中,正确的有( )
①ac>bc;②ac<bc;③ac2>bc2;④ac2≥bc2;⑤$\frac{a}{c}$>$\frac{b}{c}$
其中,正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.人体中一种细胞的形状可以看成是圆形,它的直径为0.00000156米,这个数用科学记数法表示是( )
| A. | 156×10-8 | B. | 15.6×10-7 | C. | 1.56×10-5 | D. | 1.56×10-6 |
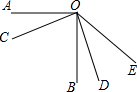 如图,已知∠AOB=∠COD=90°,∠AOC=20°45′,∠DOE=26°58′,则∠BOE=47°43′.
如图,已知∠AOB=∠COD=90°,∠AOC=20°45′,∠DOE=26°58′,则∠BOE=47°43′.