题目内容
19.若a+b=-6,ab=6,则$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值为( )| A. | $\sqrt{6}$ | B. | -$\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
分析 根据二次根式的运算法则即可求出答案.
解答 解:∵a+b=-6,ab=6,
∴($\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$)2
=$\frac{b}{a}$+2+$\frac{a}{b}$
=$\frac{{a}^{2}+{b}^{2}}{ab}$+$\frac{2ab}{ab}$
=$\frac{(a+b)^{2}}{ab}$
=$\frac{36}{6}$
=6
∴$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\sqrt{6}$
故选(A)
点评 本题考查二次根式的运算法则,解题的关键是熟练运用二次根式的运算法则,本题属于基础题型.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
11.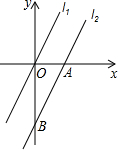 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )
 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
8.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如下表:
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加满48L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
| 汽车行驶时间t/h | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q/L | 100 | 94 | 88 | 82 | … |
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加满48L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
10.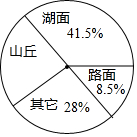 下面是我去某公园占地分布情况统计图:
下面是我去某公园占地分布情况统计图:
(1)湖面占地面积最大,路面占地面积最小.
(2)山丘占公园的22%.
(3)假设公园占地1200公顷,请填写下表.
 下面是我去某公园占地分布情况统计图:
下面是我去某公园占地分布情况统计图:(1)湖面占地面积最大,路面占地面积最小.
(2)山丘占公园的22%.
(3)假设公园占地1200公顷,请填写下表.
| 占地类型 | 湖面 | 山丘 | 路面 | 其它 |
| 占地面积(公顷) | 498 | 264 | 102 | 336 |
 的值在( )
的值在( ) C=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s的速度向点B运动,点N从点A出发,沿边AC以3cm/s的速度向点C运动,(点M不与A,B重合,点N不与A,C重合),设运动时间为xs.
C=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s的速度向点B运动,点N从点A出发,沿边AC以3cm/s的速度向点C运动,(点M不与A,B重合,点N不与A,C重合),设运动时间为xs.
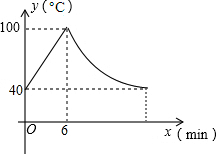 某型号的饮水机接通电源后就进入自动加热程序,水温升至100℃后自动停止加热,停止加热后水温开始下降,当水温降至40℃,饮水机再次启动自动加热,重复上述程序,一个周期内水温y(℃)与时间t(min)的关系如图所示,(水温上升过程中温度与时间成一次函数;水温下降过程中,温度与时间成反比例函数),根据图象,解答下列问题:
某型号的饮水机接通电源后就进入自动加热程序,水温升至100℃后自动停止加热,停止加热后水温开始下降,当水温降至40℃,饮水机再次启动自动加热,重复上述程序,一个周期内水温y(℃)与时间t(min)的关系如图所示,(水温上升过程中温度与时间成一次函数;水温下降过程中,温度与时间成反比例函数),根据图象,解答下列问题: