题目内容
在△ABC中，∠A=90°，AB=8cm，A
C=6cm，点M，点N同时从点A出发，点M沿边AB以4cm/s的速度向点B运动，点N从点A出发，沿边AC以3cm/s的速度向点C运动，（点M不与A，B重合，点N不与A，C重合），设运动时间为xs．
（1）求证：△AMN∽△ABC；
（2）当x为何值时，以MN为直径的⊙O与直线BC相切？
（3）把△AMN沿直线MN折叠得到△MNP，若△MNP与梯形BCNM重叠部分的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？
练习册系列答案
相关题目
6．平面直角坐标系中，三条直线l1：y=ax，l2：y=x-a，l3：y=a（a≠0）的公共点是（ ）
| A． | （-1，-$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，-1） | C． | （$\frac{1}{2}$，1） | D． | （1，$\frac{1}{2}$） |
如图，在?ABCD中，CH⊥AD于点H，CH与BD的交点为E，如果∠1=70°，∠ABC=3∠2，那么∠ADC=60°．
10．下列各式中是分式的是（ ）
| A． | 2x | B． | $\frac{1}{6}$（x-y） | C． | $\frac{x}{3}$ | D． | $\frac{1}{x+1}$ |
19．若a+b=-6，ab=6，则$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值为（ ）
| A． | $\sqrt{6}$ | B． | -$\sqrt{6}$ | C． | 2$\sqrt{3}$ | D． | -2$\sqrt{3}$ |
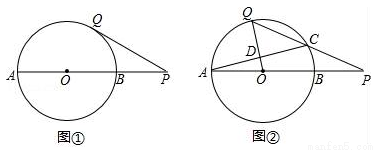
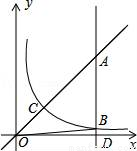
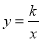（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，交x轴于点D， 
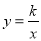与直线y=x交于点C，若OB2﹣AB2=4